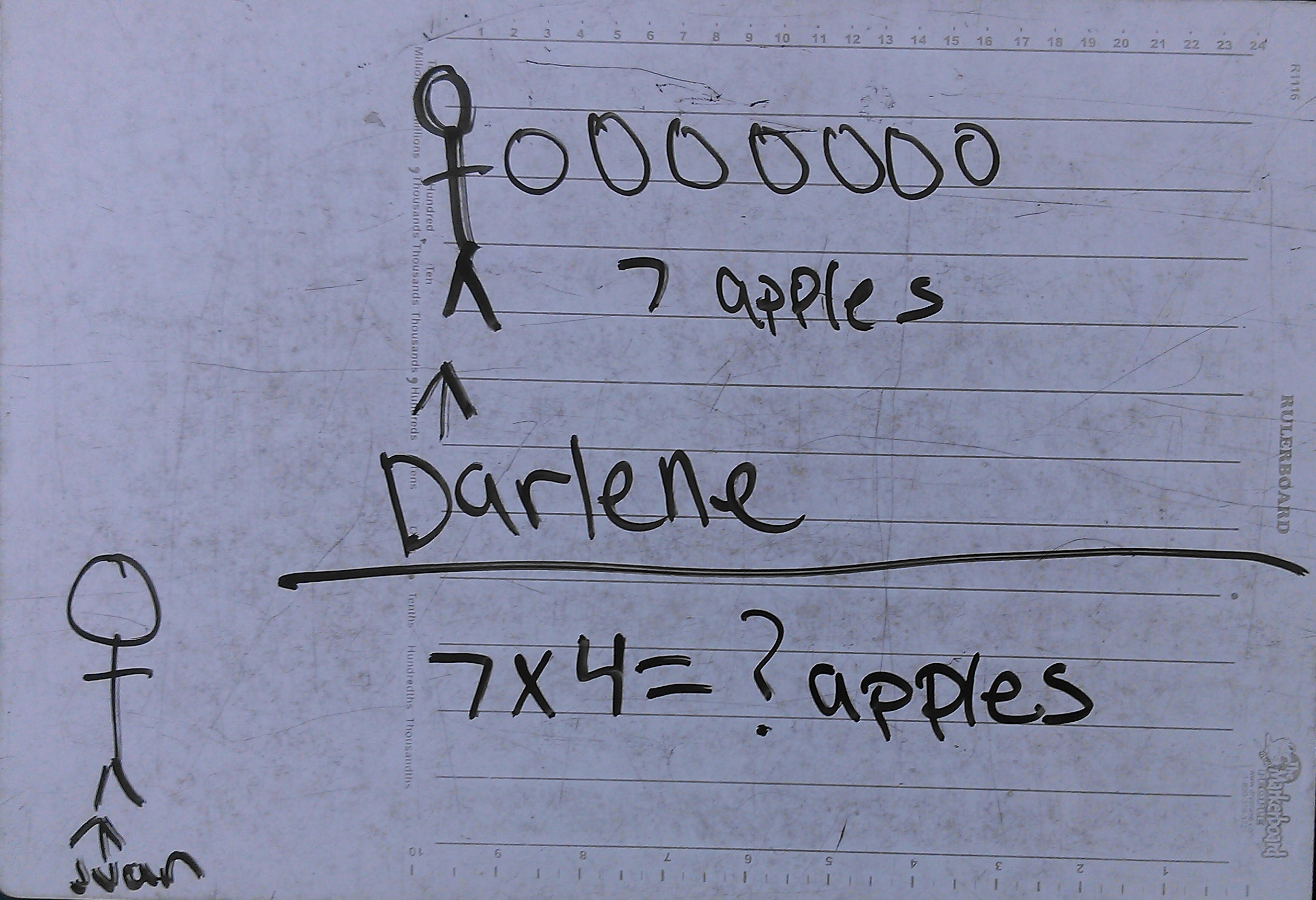Comparisons: A Little Bit More Older

Posted on by tzager

Ask any elementary school teacher, and she or he will tell you that comparison problems are much harder for most kids than operations with other actions. For example, fourth-grade-teacher Jennifer Clerkin Muhammad asked her students to draw a picture of this problem from Investigations:

Darlene picked 7 apples. Juan picked 4 times as many apples. How many apples did Juan pick?

Her students are pros at representations and skillful multipliers, but we saw a lot of this:

apples unsure

Kids who were used to thinking of multiplication as either groups, arrays, or repeated addition had some productive, furrowed-brow time ahead of them. How can you represent comparisons? How is this multiplication? How do you draw the 4?

Then they started to get somewhere.

apples groups

apples array

With each representation they discussed, Jen asked the excellent question:

“Where do we see the 4 times as many in this representation?”

Seriously. Jot that one down. It’s a keeper.

Jen and her class played with a series of problems involving multiplicative comparison, (height, quantity, distance, etc.). For each problem, she asked student to create a representation. And then she’d choose a few to discuss, asking, “Where is the ______ times as ______ in this representation?” Lightbulbs were going off everywhere as students broadened and deepened their understanding of multiplication.

Teachers often see the same struggle with comparison situations that can be thought of as subtraction or missing addend problems, like:

Marta has 4 stuffed animals. Kenny has 9 stuffed animals. How many more stuffed animals does Kenny have than Marta?

If kids have been taught “subtract means take away” or “minus means count backwards,” then this problem doesn’t fit the mold. And if kids have been taught keyword strategies, they’re likely to hear “more,” pluck those numbers, and add them together.

Knowing this as I do, I jump on opportunities to explore comparison problems with my own kids. I want them to have a fuller sense of the operations from the beginning, rather than developing too-narrow definitions that have to be broadened later. So, subtract doesn’t mean take away in our house. They’re not synonyms. I actually don’t worry about defining the operations at all: we just play around with lots of different types of problems, and I trust that my kids can make sense of them.

Yesterday, I was talking with Daphne about a neighbor visiting tomorrow. Our neighbor has a little girl, whom I’ll call Katrina. She’s about 2. We also have more awesome girls who live across the street. Let’s call them Lily, 15, and Gloria, 13. Gloria helps out once a week, and my girls idolize her. Here’s how the conversation kicked off:

Me: “If Katrina’s mother comes over to help me on Sunday, could you play with Katrina for a bit so her mom and I can work?”

Daphne: “Yes!!! We love playing with her. And she loves us. She cries when she has to leave us. We’re her best friends.”

Me: “I think Katrina feels the way about you and Maya that you and Maya feel about Lily and Gloria. It’s fun to hang out with older kids. You learn a little about what’s coming for you.”

Daphne: “Yeah. But for Katrina, Lily and Gloria would be TOO old. Like, she’d think they were grown-ups because they’re SO much older than she is. We’re older than Katrina, but we’re less older than Lily and Gloria are.”

So there’s my opportunity. She was comparing already. With a little nudge, I could encourage her to quantify and mathematize this situation. I thought I’d start with the simplest numbers so she could think about meaning first.

Me: “How much older are you than Katrina?”

Daphne: “I think she’s 2. So…”

There was a pretty good pause.

Daphne: “Are we counting on here?”

That’s paydirt.

Me: “What do you think?”

Daphne: “I think so. Because I want to know how many MORE. So, 2. 3, 4, 5, 6. I’m 4 years older than she is. Yeah. That makes sense.”

Me: “OK. So how many years older is Maya than Katrina?”

Daphne: “6.”

Me: “You didn’t count on that time. What did you do?”

Daphne: “Well, I knew that I was 4 years older than Katrina, and Maya is 2 years older than me, so 4, 5, 6. Because Maya is OLDER than me, I knew they had to be farther.”

Me: “What do you mean farther?”

Daphne: “Like, it had to be more. I was starting with 4, and then it had to be more farther apart.”

Me: “Oh! So you were trying to figure out whether to go 2 more or 2 fewer?”

Daphne: “Yeah. And it had to be 2 more, because Maya’s more older than Katrina than I am. I mean, I’m older than Katrina, and Maya’s older than me, so she’s more older than Katrina than I am. It had to be 2 MORE.”

Hot damn!

Daphne’s life might have been easier right here if she had some tools she doesn’t have yet. I’m thinking about number lines, symbols, and a shared mathematical vocabulary including words like distance or difference. Those tools might help her keep track and facilitate communicating her thinking to somebody else. But I love that we were able to have this conversation without those tools, while driving in the car where I couldn’t even see her gestures. Her thinking is there, and clear. The tools will come as a relief later on, when the problems are more complicated.

We kept going.

Me: “OK. So you’re 4 years older than Katrina and Maya’s 6 years older than Katrina. I wonder how that compares to Gloria? Is she about the same amount older than you two as you two are older than Katrina?”

Daphne: “Well, she’s 13. This is gonna be hard.”

Long pause.

Daphne: “She’s 7 years older than me.”

Me: “How’d you figure that out?”

Daphne: “I went 6. 7, 8, 9, 10, 11, 12, 13.” She held up her fingers to show me.

Me: “So how much older is Gloria than Maya?”

Daphne: “Umm…so Maya’s 8…umm…5. She’s 5 years older than Maya.”

Me: “How do you know?”

Daphne: “Because Maya’s 2 years older than me, so it’s 2 closer.”

This is the kind of problem where kids lose track of their thinking easily. Do we add or subtract that 2? In the last problem, she’d added. This time she subtracted. And she knew why!

When I glanced at Daphne in the rearview mirror, she had this awesome look on her face. She was looking out the window, but not seeing what was outside because she was so deep in thought. I wish I could have peeked inside her mind, and seen what she was seeing. Because, to use Jen’s question, where do we see the 2 years older? How did she see it? There was no time to ask, because she was onto pulling it all together.

Daphne: “So, Gloria’s a little bit more older than us than we are older than Katrina, because Gloria is 5 and 7 years older, and we’re 4 and 6 years older. But it’s pretty close.”

We pulled into the school parking lot on that one.

In our family, we count and manipulate objects all the time. Counting more abstract units like years, though, gives me a chance to open the kids’ thinking a little bit. In this conversation, Daphne was both counting and comparing years. Tough stuff, but oh so good.

The Art of Deciding, or Would You Drive Under the Overpass?

Posted on by tzager

Maya (7) asked me about this sign in the coffee shop drive-thru the other day:

IMAG3459

And so, we had a lovely conversation about clearance. Once she understood the notation, she asked, “Does that mean if your truck is 9’5″, you could drive underneath?”

That’s just gold.

I said, “Well, it depends how confident you are in the two measurements. Are you sure the clearance is exactly 9’6″? Are you sure your truck is exactly 9’5″?”

She thought about it a while, and decided that was too close for comfort. We brainstormed a nice list of sources of error while we waited in line:

  • What if the tires weren’t as inflated when you measured, and then you filled them up with air?
  • What if the person measuring made a mistake?
  • What if the tape measure was a little bent?
  • What if they didn’t get to the very top of the truck, like an antenna or exhaust pipe sticks out or something?
  • What if there’s ice on the road, so your truck sits a few inches higher? (There was ice, in fact. Happy Thanksgiving.)
  • What if they’ve paved the parking lot since they made the sign, so now the road is higher?
  • What if whatever is overhead is curved, and the 9’6″ is the highest part, even though it should be the lowest?
  • What if it was really almost 9’6″, so they just went to the next closest number to make it even, but it’s really a little under. And what if the truck is really a little over 9’5″, but they went to the next closest number to make it even too? It could be a lot less than an inch!

That last one was Maya’s, and it’s my favorite, probably because I’ve been spending time with the (unfortunately out of print) 1986 NCTM handbook Estimation and Mental Computation lately. It’s a worthwhile read about an important and neglected topic, and I hope an update is in the works this (ahem) century. Peter Hilton and Jean Pederson caught my eye with this quote in their article, “Approximation as an Arithmetic Process”:

It is an extraordinary triumph of the human intellect that the same number system may be used for both counting and measurement. Nevertheless, we argue that the arithmetic of counting is not at all the same as the arithmetic of measurement; and that the failure to distinguish between these two arithmetics (which one might call discrete and continuous arithmetic) is responsible for much of our students’ confusion and misunderstanding with respect to decimal arithmetic and the arithmetic of our rational number system (57-58).

That’s a doozy, and it’s been rattling around in my head for a while. The authors point out that, in counting, 3.00 = 3, but in measurement, 3.00m ≠ 3m. Do we make a big enough deal about this distinction in class? I’m thinking no, not by a long shot.

Hilton and Pederson make the case that all measurements are approximations, and we should teach them that way. This is a really interesting idea. What would happen if, from the outset, we were honest about the inherent uncertainty and decisions made in every measurement? What if we stopped referring to the “actual” measurement, and instead talked about the closest approximations we could get, or a range of reasonable measurements?

Thus there are situations in which we round off in view of the accuracy we NEED and situations in which we round off in view of the accuracy we can genuinely GET—and, of course, situations in which both kinds of consideration apply. The technique of rounding off is a familiar one, but we emphasize that the technique, easy in itself, is based on the nontrivial, nonalgorithmic art of deciding the appropriate level of accuracy (58).

Teaching the “art of deciding the appropriate level of accuracy” is a far cry from a worksheet with the directions, “round off to the nearest hundredths place.” The art of deciding involves the idea of authorship, which runs headlong into the myth of math as objective truth. The art of deciding means there is always an interval of reasonable answers to a measurement problem, not just one “right” answer printed in the back of the book. The art of deciding is empowering; the opposite of regurgitation.

As a student, I loathed the dreary lessons on significant figures, uncertainty, and measurement error. They were full of hierarchical rules and tedium and a complete absence of intuition and sense-making. Booorrriiiing. As an adult, I’m baffled that we somehow make boring this element of mathematics that involves a little bit of mystery, the explicit acknowledgment that sometimes we can’t know no matter how hard we try, and an honest admission that we make decisions when doing math. How do we kill it? We mask the interesting parts because we, the teachers, are the ones practicing the art of deciding. We are the ones who choose whether to measure to the nearest 1/2 inch or millimeter or gram. We leave the trivial implementation of our decisions to our students, but we keep the decisions for ourselves. Not good.

So, I left the deciding to Maya. Would you drive your truck underneath if it was 9’5″? She said no. I asked, what if your truck was 9’3″? She said no.

“I don’t think I’d be comfortable going under unless my truck was under 9′. Then I’d be confident I wouldn’t hit.”

She’d decided that 6″ is a reasonable margin of error, so she wouldn’t end up like these guys.

You might decide on a different amount of wiggle room. That’s cool too. Deciding is personal. It’s an art.

Appendix:

If you end up wanting to pursue any of this with kids, here are a few things I found helpful:

http://www.democratandchronicle.com/story/watchdog/2014/08/20/rr-bridges-and-trucks/14338865/

http://safety.fhwa.dot.gov/geometric/pubs/mitigationstrategies/chapter3/3_verticalclearance.cfm

https://www.youtube.com/watch?v=o8Z1K37SHbE

http://www.truck-drivers-money-saving-tips.com/low-clearance.html

And here’s a “real-world” answer, courtesy of David Wees and Sky Wyatt:

Screen Shot 2014-12-01 at 9.59.21 AM

UPDATE: September 2015. Somebody too tall drove under and broke the thing!

IMG_20150912_110710_421

The Same Amount of Tall

Posted on by tzager

My 5-year old daughter, Daphne, was looking out the car window when she laid this question on me:

“I’ve been wondering something. If there’s a whole of a tree, and half of a tree next to it, what do you call it? A whole half?”

At the next light, I turned on my phone and recorded our conversation. What follows is a word-for-word transcript. It’s one of my favorite math discussions ever, because I learned so much about her thinking.

“First of all, tell me about the half of a tree. How do you know it’s a half?”

“It’s a stump.”

“It’s a stump?”

“No. I mixed up the word. It’s a trunk.”

“It’s a trunk. OK. So tell me how you know something is half again. What does half mean?”

“Half means they are even pieces and you cut one of the even pieces up and you leave the other one, then they’re even, and that’s half. The one that’s down and the one that’s up without the other one is half.”

“OK. I have a whole lot of questions. Are you ready? This is the first one. Tell me what you mean by even.”

“Even? They’re both the same amount of tall.”

“They’re both the same amount of tall.”

“Yeah.”

“Whoa.” (Long pause.) “You’re talking about trees. What about wide? Do they have to be the same amount of wide also, or just the same amount of tall?”

“Just the same amount of tall.”

“Just the same amount of tall. OK. So here’s my next question about halves. How many pieces do you have?”

“Only two!”

“Only two. How come?”

“Because you cut one off and leave one on.”

“And that’s halves?”

“Yeah.”

“What if you cut it into three pieces that were the same amount of tall?”

“That would be quarters.”

“How come?”

“Because they just are!”

“What’s a quarter?”

“A little bit of something.”

“A little bit of something. What if I cut it into, like, 20 pieces of the same amount of tall?”

“That would be like…inches.”

“Inches! OK. So, it goes halves, the next smallest is quarters, and then the next smallest is inches?”

“Yeah.”

“What if I cut it into, like 1,000 pieces?”

“It would be just specks.”

“Specks…Hmm. And you said it doesn’t matter, like, I’m looking at that tree over there, and it’s fatter at the bottom–the trunk is fatter at the bottom and skinnier at the top–but the top has lots of leaves and the bottom doesn’t. Does any of that matter, or it’s just the same amount of tall?”

“Where?”

“That tree with the orange leaves.”

sugar-maple-1-547x547
(It wasn’t this tree, but it was a sugar maple like this one.)

Long pause.

“That one has too many branches.”

“OK. So what kind of tree does it work for?”

“Trees…like that one!” (Pointing at a sapling.)

“OK, so what is it about that tree?”

“It’s smaller and it doesn’t have very many branches.”

“Hmm. What sorts of things can we cut in half?”

“Bread…flags…” She trailed off, and we were quiet for a while. I decided to revisit the thirds and quarters idea a little more.

“Can we think about cookies for a second? We made cookies yesterday. If you and Maya and I shared a cookie and we all had the same amount of cookie, how much cookie would we each have?”

“A quarter.”

“How come?”

“Because that’s a little bit of sugar and it’s all the same.”

“How many quarters does it take to make a whole cookie?”

“It matters how big the cookie is.”

“Tell me about that.”

“It would be a lot of pieces if it was a huge cookie, but just a little bit of pieces if it was small.”

“So, if I broke it into pieces so you got one piece, and Maya got one piece, and I got one piece of a small cookie, and then I took a big cookie, and I broke it so you got one piece, and Maya got one piece, and I got one piece of the big cookie, it would take different numbers of pieces, you’re saying?”

“Yes. Because they’re bigger.”

“So if it’s a bigger cookie that the three of us share evenly, we have more pieces?”

“Yeah.”

We kept going for a while longer, but you get the gist.

I love this conversation. I love it partly because it’s evidence that kids are mathematical thinkers who come to us full of ideas. Some of the ideas hold up to scrutiny and some don’t. Some are misconceptions we’ll need to address, and some are deep conceptual understandings and experiences we’ll want to build on.

What does Daphne know? We can divide wholes into parts. We can keep dividing into lots of pieces, and the different pieces have different names. We can use fractions to share. And, most importantly, we can look out the window and see mathematics, and wonder, and have conversations about our ideas.

What does Daphne not understand? Units, although I adore her sequence of halves, quarters, inches, and specks. She has a lot of fraction ideas intertwined. For example, even though she thinks we can have halves of big things, like trees, and halves of smaller things, like flags, she thinks a quarter is a size, and it’s small. There’s a lot of room to explore the distinction between the number of pieces and the size of the pieces. She has developing ideas about measurement and the idea of identifying a dimension: the “same amount of tall” goes in my math Hall of Fame. Volume didn’t occur to her here. That’s OK.

In case you’re wondering, I didn’t “address” any misconceptions, and I’m not worried about any of them. My goal here was not to have Daphne identify fractions with accuracy, or learn any definitions, or figure out how to measure something as complex as a tree, or answer my questions with an expected answer. My goal was to join her wondering, listen to her ideas, help her clarify her thinking here and there, and gain a deeper sense of how she’s seeing the world. I look forward to revisiting fractions and measurements with her many times, and to bearing witness as she makes sense of these ideas. It’s my privilege, as a parent and a teacher. See, math is fascinating. And Daphne is fascinating. Together? It’s the best.