I’m so stinking lucky. I’m working with an amazing staff at a lovely school over weeks, months, and years, and I learn so much every day we have together. Yesterday, I spent my afternoon with the K-2 teachers, and we continued our ongoing discussion about number lines.
The kindergarten teacher at this school thinks so powerfully about how her kids think! The week prior, she’d told the rest of us that she’s been modeling using number lines as representations and tools, but she wasn’t sure how to help kindergarteners really own the number line. I loved that thought.
I turned to some of my favorite sources to see what I could find about introducing number lines. Kassia Omohundro Wedekind, thinker, writer, and kindergarten teacher extraordinaire, helped me tremendously. She emphasized the importance of teacher modeling, a la, “This is one way you could show what you just did on a number line.” She suggested using lots of board games where kids move game pieces and count jumps. She brought up developmental issues around drawing the number line with paper and pencil, and how it would be hard to tell if kindergarteners were struggling because of the math or fine motor skills. She talked about building a giant number line.
The teachers and I had also thought about constructing a big number line, so I also wrote Malke Rosenfeld, who is always thinking creatively about the intersection of math, dance, and painters’ tape! She was generous with her time and gave me a lot to think about. My biggest takeaway from our conversation was to avoid turning a giant number line into a giant worksheet. I can see how easily we could have moved right to having the kids “acting out” what we did with markers and pencils on paper. That would have been unfortunate. As Malke wrote me, “Working at moving-scale is really about opening up possibility for new insights about math ideas that is not accessible at hand-scale or in symbolic form.” Hmm. That’s interesting.
I also turned to my bookshelf, and spent a fair amount of time looking for good thinking about introducing the number line as a model. If anyone has good references, I’m all ears. I found most books just jump into using the number line, without thinking about how students would make sense of it. I did find a really interesting chapter in Cathy Fosnot and Maarten Dolk’s Young Mathematicians at Work: Constructing Number Sense, Addition, and Subtraction called “Developing Mathematical Models.” They focused on contexts for learning the number line, and included examples using bus stops and city blocks. Those examples were both from schools in New York City, where students have a tremendous amount of experience with buses, city blocks, and subways—all rich contexts for discussing the number line. The school where I’m working is in a small town in rural New Hampshire. The kids don’t ride buses or subways, and the numbered streets in the town center start at 2nd street and end at 4th street. These contexts weren’t going to work at all!
None of us could think of a familiar context for number lines in these students’ home lives. (If anyone has ideas for contexts, I am all ears. Please leave them in the comments.) I still felt like it was important to connect to something the kids were already doing or thinking about, so I went into the kindergarten room to look for opportunities. That’s when I saw this chart:
The teacher told me they keep track of how many days they’ve been in school using this chart. Just that morning, she’d added the second piece because it was day 121, and there’d been a lot of conversation about it. They also use the chart to look for patterns in number, practice skip counting, etc.
When we met as a team, we talked about using this chart as context. We thought about asking students what would happen if we stretched the numbers out so they were all in a line?
A quick thought about “real world” here. This chart is very different from bus stops and city blocks in that it’s already an abstract representation of numbers, rather than experience from students’ daily lives. What mattered to me wasn’t the “real-worldness” or not of the context, though. What I wanted to do was give students a chance to connect one idea to another; to make a bridge from something they knew to something new. Seeing math in the world around us is one huge type of connection (to borrow literacy terminology, it’s a math-to-world connection). Making connections from one mathematical idea or representation to another is also a huge type of connection (math-to-math, right?). Some of the best math lessons I’ve ever taught have involved comparing two different representations. I was happy to start with the chart.
As a team, we made some decisions:
- We’d have the kids work in small groups on long number lines, and see what happened.
- We decided that each group should pick a starting number off the chart. It could be any number they liked, but they had to come to consensus on that number.
- We decided having several different sections of the number line would work better than trying to have the groups each take a segment of one long line, and then attach them together somehow. An added bonus was we want students to know they can zoom in on any section of the number line and use it. They can start and stop anywhere, rather than starting at zero or one. We wondered if this approach might help them with counting on?
- We’d ask students to put eleven numbers in order on their number line because we wanted them to be able to make ten jumps.
- We’d give students sticky notes to use to work out their ideas, and then tape when they were ready.
- We decided to line the tape up with the floor tiles and see if any students noticed their regularity, and used them to place their numbers.
We expected students would struggle working together. That’s OK. Teaching how to work together is part of teaching, and teaching math. We expected sequencing might be hard for kids, especially because the chart is organized vertically. Otherwise, we weren’t sure what to expect!
All groups started the same way:
- They chose their starting numbers first (1, 2, 6, 13, 14, 15, 121—this lesson was inherently differentiated in that regard).
- They wrote their numbers on sticky notes (sometimes after arguing, sometimes after taking turns).
- They sequenced their numbers correctly (some groups used the chart to figure out the sequence—awesome).
- They placed them side-by-side on their number lines, all scrunched up on one end:
Fascinating! We started asking kids, “Can you use more of the line?” That’s when the really interesting discussions started. One group immediately understood they could put more space in between their numbers. They started by inserting a “finger space” like they put between words. When they’d finished, they still had lots of line left. They tried again, this time inserting a “hand space” between sticky notes. Still too much room. At that point, they noticed the tiles, and decided to use them.
Their line was one tile longer than they needed, however, which brought up some interesting questions.
When we pointed out that the space between 15 and 16 was wider than the other spaces, the kids discussed what to do. They ended up asking if they could have a 17 so they could go all the way to the end but make them even. Great solution.
At this point, we decided to have the kids take a “walkaround.” We wanted them to learn from each other’s ideas. After kids had looked, we heard students say, “We could spread them out more!” Great! What we noticed, though, was most groups spaced out their numbers, but didn’t distribute them evenly.
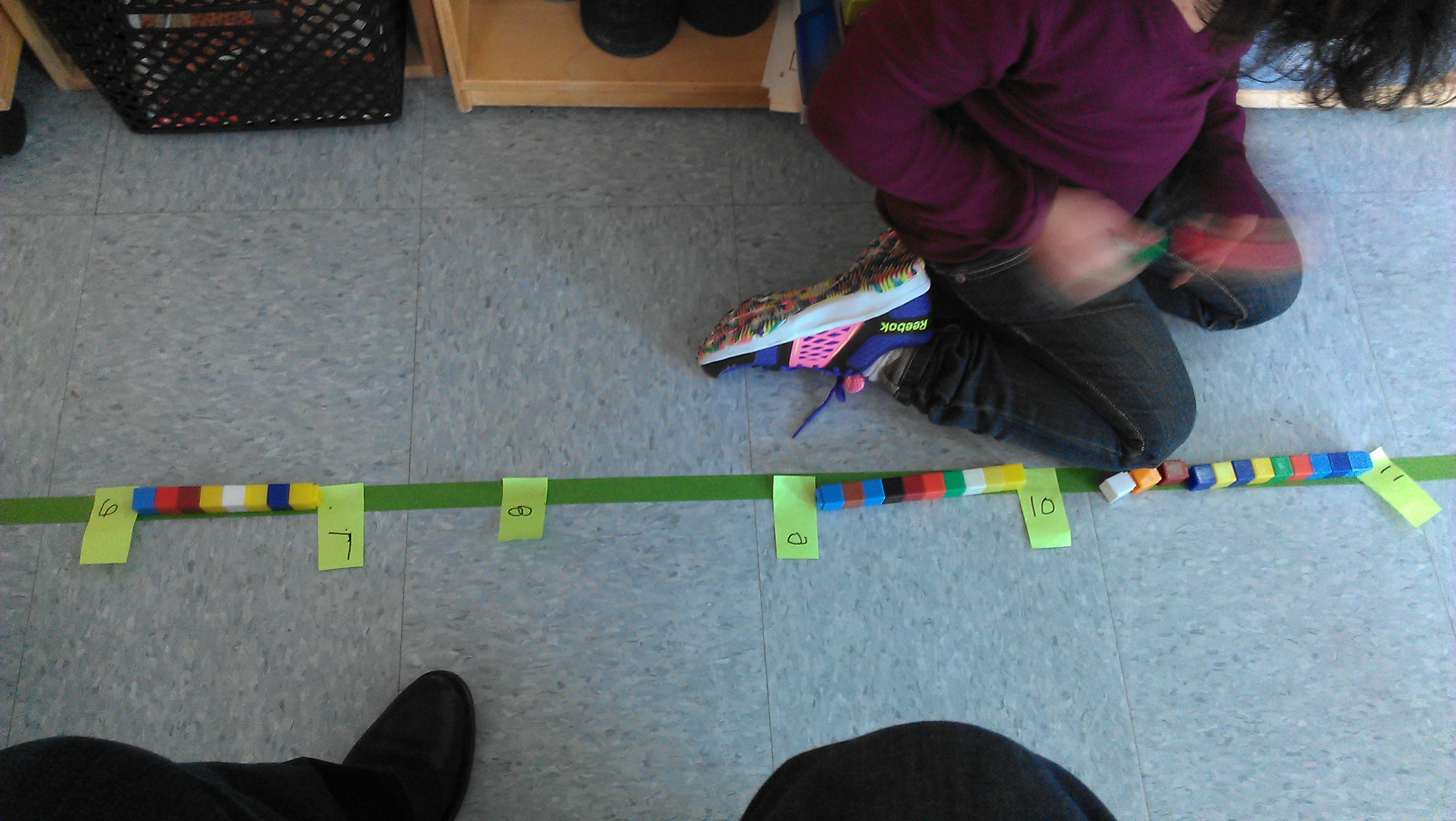
Teachers ended up pointing out the uneven spaces to kids. Some of the kids were fine with the spaces being uneven, while others wanted to revise their thinking. In one group, a student used his sneakers to prove the spaces were uneven.
“See? On this one, my foot touches the two numbers. But on this other one, there’s some extra sticking out.” I was thrilled with this development. I hadn’t really thought through the measurement aspect of this lesson, but here it was. A groupmate of his took out some cubes, and snapped together a stick of them. I thought she would use her cube-stick as a consistent unit, and space all the numbers that distance apart. Instead, she created lengths to match each interval.
Not what I expected, but totally cool too.
We paused the kids here for just a minute, and had students share how they were using tools they found in the room—floor tiles, feet, cubes—to measure. We gave students another chance to work on their number lines. One group loved the feet idea, and successfully worked together to make an evenly spaced number line using their bodies.
I was so happy, because now there were at least two number lines with evenly distributed intervals of different lengths: the one marked off by tiles, and this one marked off by one student’s foot. What a great opportunity for kids to compare and connect! And, of course, I love me a good use of non-standard units.
Other groups taped their lines down with irregular intervals.
I’m realizing how powerful it is to use removable painters’ tape to make these lines. I wonder, as the kids explore with their lines in the coming days, if these groups will want to revise their thinking. The teacher works hard to create a culture where revising thinking is a big part of doing math, so it’s possible.
When we discussed the lesson afterward, we were happy with a lot of it. We had all watched the kids sliding up and down the tape, moving from one side to the other of the line, and jumping from number to number. Everyone was happy to keep the lines down on the floor for a while, and see what happens. We talked about different ideas to create more opportunities for the kids to play with body-scale number lines, and decided to add a permanent one all the way down the K-2 hallway. The principal is going to have some number lines and hash marks painted on the blacktop outside, and teachers and students will be able to use sidewalk chalk to write different numbers on them. They’re going to paint some board-game paths outside and get some giant dice. And they’re going to add numbers in each stairwell, going up and down (yay, negative numbers!) from the 0 level.
Students asked great questions during the lesson. For example, one student talked about their first number line, when the numbers were squished together. She asked, “If we kept the numbers that close together and just kept adding sticky notes, I wonder how high the numbers would go.” Me too!
Our one discomfort was we felt like we imposed the idea of regularly spaced intervals on the kids, without really developing a need. We had planned the lesson quickly, and were much more focused on ideas of sequencing and magnitude than we were on measurement. We didn’t anticipate that the spacing of the intervals would be the big issue. Now that we’ve seen what happened, we’re all left wondering how we could have the kids realize the numbers need to be evenly spaced? What would help them see a reason?
Ideas?
—
Update: Part 2 is posted.