Update 12-9-15 Since pressing publish, I’ve thought of much better titles for this blog. Take your pick:
The Rhythm Method
or
Mathematicus Interruptus
—
I returned last night from a thought-provoking PCMI weekend workshop. A+ professional development, friends. Seriously, if you have a chance, go. Huge thanks to Tina Cardone for organizing it.
Each day, we alternated doing lots of math with facilitator Brian Hopkins and reflecting on our practice with facilitators Cal Armstrong and Jennifer Outz. Plus we socialized, shared ideas, and learned from PCMI alumni. It was a great mix and there are many things I could blog about, but I want to focus on some of Brian’s choices that I found surprising in the best way possible. He really has me reflecting on my practice.
Spoiler alert: I’m going to introduce some math problems – problems we thought about with other teachers for long stretches of time. After each problem, I’m going to have to give away some of the mathematics to make the point I want to make. If you want a chance to think through the math yourself, pause after each picture. Go play. Then come back. If you keep reading, you’ve been warned. You’re missing out on some of the fun.
Assurance: I’m going to be using some math vocabulary, ideas, and representations that were new to me and I spent many hours exploring this weekend. They’re still tentative for me. If you don’t take the time to figure out the math and you don’t know it already, that stuff won’t make sense as you read. Don’t worry about it for these purposes. I’m not trying to recreate PCMI here. I’m trying to make a larger point that you can totally get even if you skim over the math. So skim away, especially in this first bit. Resume close reading after the circular pennies picture.
The first morning, we started with a penny game. (Thanks, Heather, for tweeting these out!)
We tested what would happen if we had different numbers of pennies or were allowed more moves. We found that multiples of 3 were very important if we were allowed to move 1 or 2 pennies. Multiples of 4 were very important if we were allowed to move 1, 2, or 3 pennies. Brian encouraged us to think about these ideas in terms of modular arithmetic, which we’d been told was going to be a focus of this weekend. My hunch is they chose this topic knowing it was outside of most of our comfort zones. Perfect. It certainly was new to me. I went in having no idea what 2mod3 meant. By the end of the morning, I think lots of us were becoming more comfortable with mod notation and thinking. Brian closed the session with a good laugh over Survivor’s 21 Flags game.
After a reflection session and lunch, Brian passed out this page of primitive Pythagorean Triples. He asked what we noticed and wondered, and encouraged us to play with mods the way we had in the morning.
So, what do you notice and wonder? What patterns do you see? What conjectures can you make?
We had all kinds of observations about the ones that were one apart or two apart, different ways to generate subclasses of triples, and what was going on with the evens and odds. Super fun. After the group share out, our group started looking at other group’s conjectures that each triple had a multiple of 3, a multiple of 4, and a multiple of 5. This got us going again with mods, and the squares of mods.

When we stopped, my group was trying out mod8 to see if that helped. I’m still not sure why, but it was fun.
When we arrived the second morning, Brian had a new challenge for us:
My partner and I tried and tried to explain this game using mods.
We failed.
The pair next to us was exploring a different technique. They found that the player who forced their opponent to face a symmetric situation won every time, as long as they kept resetting the symmetry. I really encourage you to try this one. It’s lovely and satisfying.
Brian pulled us together and asked what we found. Consensus was that mods were unhelpful, and that symmetry was the more powerful idea here.
This was the most exciting moment of the weekend for me, pedagogically. The way I thought about it was that Brian disrupted the predictable, pitter-pat routine of math class. Up until this moment, all signs pointed toward mods. I assumed each new activity would build on what we’d done before in this familiar story arc. We’d deepen, add nuance, try new aspects and applications. I did not expect to have Pennies II be totally different than Pennies I, and not involve the handy new tool we’d just learned.
I started scribbling in my notes. When do we ever do this? When do we teach a new tool and then introduce a similar task where this tool is not helpful? When do we teach kids the limits of the tool right from the beginning?
What I see in schools is we cue kids to know what tool to use. If we’re two weeks into a unit on fractions and we give them a story problem, the kids figure fractions are involved. If the name of the chapter is “Multiplying Two-Digit Numbers” and it’s written on the bottom of the worksheet, the kids are going to assume they should multiply some 2-digit numbers. If we’ve written an objective about linear equations on the board, kids figure the answer is going to involve linear equations. If my new tool is the hammer that divides fractions, I’m going to use that hammer until my teacher tells me it’s time to switch hammers.
At PCMI, Brian disrupted that process for me. He gave us a new tool, and then gave us a problem where it didn’t apply. Blew my mind. Next up, though, was Pennies III, which he referred to as 11 plus 1, and later told us was called Kayles. It has the same rules as Pennies II, but the pennies start out in this arrangement.

At first, I thought, “Oh, we’re back in the rhythm. I bet this game will give us some amazing synthesis of mods and symmetry. I get it. I see his plan.” Because that’s how math classes normally work, right? I’ve cracked that code.
My table worked and worked and worked at this problem and couldn’t come up with any good rules using mods or symmetry, or anything else for that matter. When we got back together, Brian told us this problem has been around forever and wasn’t analyzed well until computers were invented. It turns out there are no elegant solutions. It’s just a messy, case-by-case thing. There were some groans in the room. Not from me. I was delighted because he’d disrupted the rhythm again. He’d surprised me.
We headed downstairs to set up for the Josephus problem. The rules he played in this version were that Josephus was going to count by 3s and kill whomever he landed on. He was also going to be in the circle. So where should he stand? Which position will be the last one standing?
Brian’s shorthand for this problem was “Duck, Duck, Die.” He began killing us off, round and round. With 29 people, player 26 survived. With 20 people, player 13 survived. What was going on here? I heard participants say, “What does this have to do with the pennies?”
Over lunch, participants tried out different numbers and Brian synthesized the data.

What do you notice? What do you wonder?
We had lots of questions and observations. Fun. But then we got to the meaty question of can you predict the solution for any number? What do you think the answer was? What do you think I thought the answer was?
If he went by typical math class rhythm, the answer would have been some marvelous synthesis of all we’d done. It was the afternoon on the last day. So could he tie together modular arithmetic and symmetry and something wise from Kayles and Josephus? Would he wrap it up in a neat, satisfying bow?
By this point, I had come to expect surprises from Brian, so I really didn’t know what was going to happen. It turns out this problem has to be solved recursively. He had a clean, recursive approach to do it, but people were unsatisfied and wanted a closed formula. He gave us this “big ugly thing.”
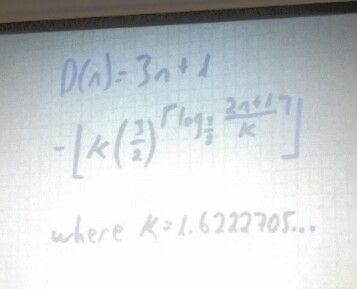
I don’t know what it means either. I do know we all cracked up when he revealed the constant. It turns out you have to solve the problem recursively to use the big ugly thing anyway, because that’s how you can calculate κ to enough digits.
Brian talked to us about how not everything in mathematics is solvable in a nice, neat formula. Sometimes this is how it works out.
I can’t tell you how satisfying I found it that there wasn’t some “satisfying” synthesis in the end. I mean, I love making connections. I love thinking relationally. But not everything connects nicely. In math class, we often create an artificial story arc where one thing leads to the next and then the next in this nice flow. We leave out the part of the story where mathematicians struggled for hundreds of years between these ideas we’ve connected in 45 minutes. We leave out the part of the story where mathematicians aren’t told what tool to use when they attempt a problem. They might try this or that. Maybe mods are helpful? Nope. Symmetry? Nope. Should I try to graph something here? Maybe that will be illuminating?
What I’m thinking about most, though, is that we teach in this familiar rhythm – this unit is factoring and every question will be solved using factoring – almost all year long. And then we’re frustrated when kids don’t “transfer” what we’ve taught them in novel situations. “We covered that!” we yell, when we see they didn’t get the factoring question right on the big state test because they didn’t recognize it as a situation where factoring would be helpful. We shouldn’t be at all surprised. We’ve been cuing them all along. The tool of the week is tables, or skip counting, or measurement. Attention everyone, the new tool of the week is negative numbers, or symmetry, or finding the intercepts. Without the cuing, where are they?
Some of this is for good reasons. It’s important to dig into ideas with depth and connect them. I’m not saying to jump around willy nilly. But I wonder if we can learn something from Brian? Next time you teach a tool, how about giving students a chance to figure out when it doesn’t help as soon as they’ve started figuring out when it does? That would give them a fighting chance of deciding when it might be helpful in novel situations. Brian’s way to help us think about the usefulness and limitations of our new gadget was to give us seemingly related problems that were actually quite different, mathematically.
I’d love to put our heads together and think about content examples in the comments. Pick a concept. How could we use Brian’s technique?
I keep thinking about a snippet of an Ira Glass talk from 1998 that has always stayed with me. He was talking about the shortcomings of the rhythm of a typical National Public Radio news story, which led him to create This American Life:
And there was something dull about the rhythm, to me as a radio producer, where every story was set up so there was a little bit of script and then you’d hear a quote, and some script and then some quote. And radio, you know, functions a lot like music, even though it’s speech. It had this very predictable rhythm.
And we never get to know any of the characters, enough to feel anything or empathize in any way or to be amused or to feel angry or to be surprised.
This weekend, I felt things. By disrupting the typical rhythm of math class, Brian gave me a chance to feel amused and confused, surprised and delighted.
It’s really worth thinking about how we can do that for our students.