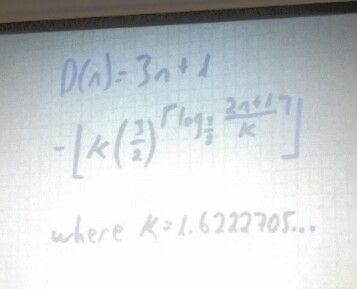One of the things I think about is the relationship between teaching math and the physical stuff that goes along with teaching math. This relationship gets distorted sometimes.
For a while, the elementary world got all kinds of swept up in manipulatives. All lessons became “hands-on” because somehow “hands-on” led to “minds-on.” Deborah Ball’s classic Magical Hopes article does the best job I know exposing the flaws in this stance. If you haven’t read it, by all means, click that link and read it right this second.
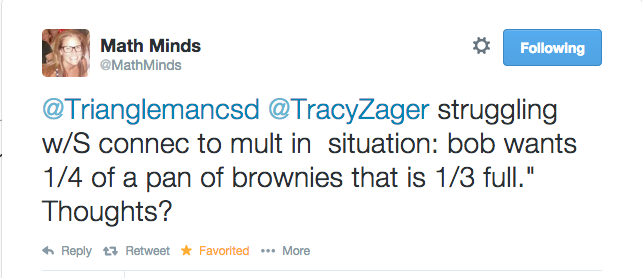
People sometimes get hung up on tech in the same way. Recently, I had the chance to share some outstanding work Kristin Gray got from her students when she asked them to take out their notebooks and write down what they were wondering about doubling and halving. They’d been working on 14 x 25 = 7 x 50. Check out these conjectures:



I mean, so great.
Both times I shared this work, people oohed and aahed, and then asked the same question: “Could you use tech to do this? Maybe a google doc?”
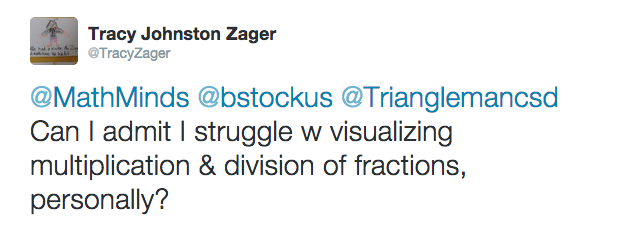
I have to confess, I don’t understand this question. With paper and a pencil, students were able to shift back and forth between words and numbers effortlessly, much faster than 11-year-old kids can type. If they’d wanted to make a quick sketch or doodle (perhaps an area model, in this situation), they could. They didn’t have to lose their train of thought while hunting through their device’s symbols for ÷ (an obelus, for fellow #wordnerds). The only apps I know that allow students to think and write so freely are apps that turn tablets into $800 notebooks by letting you write on a screen with a stylus.
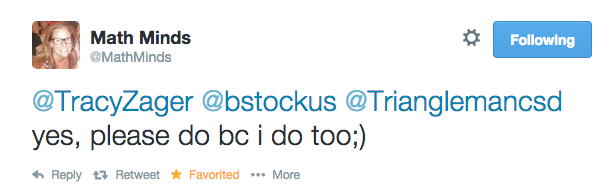
I kept wondering, what’s the value added there? What’s the rationale for adding tech? What can it do for you that cheapo paper notebooks can’t?
That’s the question I ask myself about tools, in general, whether they require charging or storage in a plastic tote. What will they do for the mathematical teaching and learning here? Sometimes, the answer is not much. Other times, A LOT.
This year, I did something new in my school. My principal and I made it a priority for me to work with our paraprofessionals. These colleagues are overworked, underpaid, undertrained, and almost never supported to go to PD. Yet they’re responsible for educating about 20% of our students–the neediest 20%. So, this past year, my principal worked out a schedule where, one week per month, I had all the paras in two different shifts on Tuesday and Thursday afternoons. Over the year, we did a book study of the second edition of Children’s Mathematics. I chose it because it’s the foundation of everything in elementary math. The book and its embedded videos teach educators how students think about the operations, and how that thinking progresses. They also teach educators to listen closely–and quietly–to students while they think through problems. Given that the paras had been jumping in too quickly to tell or spoonfeed or direct kids, I wanted them to start learning how to tolerate wait time, how to trust that their students have mathematical ideas, and how to listen as a core part of teaching mathematics.
[Update, June 30 2017. I received a note from one of my colleagues–a proud paraprofessional–today. It was a hard note to read, but I am so grateful that she wrote. She taught me a ton. I am leaving the blog intact so you can see what I wrote, and what I learned. Let’s take a look at that paragraph again, but I’ll fix it, and then make changes throughout:]
This year, I did something new in my school. My principal and I made it a priority for me to work with our special education team, including certified teachers, therapists, and paraprofessionals. These colleagues are overworked and underpaid, and there are many demands on their time because they frequently have trainings about specific disabilities and student needs, as well as IDEA compliance, not to mention the meetings required for IEPs. undertrained, and almost never supported to go to PD. Yet they’re These colleagues are responsible for educating about 20% of our students–the neediest 20%–but both the literacy coach and I get less time with them than we do with the classroom teachers. So, this past year, my principal worked out a schedule where, one week per month, I had all the paras the full special education team in two different shifts on Tuesday and Thursday afternoons. Over the year, we did a book study of the second edition of Children’s Mathematics. I chose it because it’s the foundation of everything in elementary math. The book and its embedded videos teach educators how students think about the operations, and how that thinking progresses. They also teach educators to listen closely–and quietly–to students while they think through problems. Given that I’d observed that some of the paras had been jumping in too quickly to tell or spoonfeed or direct kids, I wanted them to start learning how to tolerate work on their wait time (which we all always need to work on). I’d spent a few years working with the classroom teachers, reading the same book (Children’s Mathematics), encouraging them how to trust that their students have mathematical ideas, and how helping them learn to listen as a core part of teaching mathematics. I wanted the special education teachers, therapists, and mainstream coaches to have similar opportunities to work on their listening.
I also knew that digging into students’ mathematical ideas would allow me to get the parasspecial education team digging into the mathematics itself. One para loves math and I knew she’d be game, but many were reluctant and some were downright hostile to the idea of this year-long focus on mathematics. I had my work cut out for me last fall.
Fast forward to June, and I gotta tell you, I loved my time with the paras special education team. I think it’s some of the most important work I’ve done in the building and I can’t believe it took me so long to get there. We built a safe space and strong relationships and, most of the time, they got more and more willing to try new ideas, wonder about why things worked, and make sense for themselves. I hope they understand that I’m sharing this story partly to encourage my fellow math coaches to think about how they can support their special education colleagues, partly because it helps me make my point about tools, and partly because I’m so proud of the growth I saw over the year, and want to share it. I hope I’ve done the story justice, and I hope, if I haven’t, they’ll tell me. Nothing matters more than the trust and safety we’ve built together.
One observation I’d made over the year was that several parascolleagues openly despised both the area model and the related partial products strategy for multiplication. They didn’t understand why anyone would do that, and were resistant to multiplying any other way than the standard algorithm. As our year drew to a close, I wanted to devote time to multiplication of double-digit numbers and see if I could get anywhere with this animosity toward these two essential multiplication strategies. I knew that if I just drew or recorded the strategies with equations on chart paper, I would lose them. I’d learned that lesson the hard way, and wanted to avoid the shut down I’d caused before. So I needed something. I needed a tool that would unsettle our typical patterns.
In this case, I reached for graph paper. I handed them each a rectangle of graph paper and asked them, “How many squares are there?” Note, I did not use the word “multiply.”

Nobody shut down. Everybody got to work, and I got a great range of strategies, including the ones above. (The graph paper was 14 x 21, if that helps.)
Man I love a variety of strategies. It’s just the best. Now I had a whole range of decisions to make about where to go from here. (If you want a thoughtful discussion about that decision-making process, you need to read Intentional Talk. It’s had a huge impact on me.) There were a number of things I could do, and a number of competing goals in my head. A few of them:
- I needed to explicitly connect what they did with the graph paper to multiplication.
- I needed to get them more comfortable with representations of what they did with the graph paper, both in pictures and numbers. Optimally, they’d be the ones recording, not me.
- I needed to expose some rich mathematics by digging down into one of these, or by drawing connections among a few of them. Which ones?
- I needed to take this opportunity to highlight the fresh mathematical thinking from some
parascolleagues who have had negative histories in math, who started out the year reluctant but dove into this problem bravely, and who still needed support to see themselves “as math people.”
- I needed them to explain their strategies to one another so they could put words to their own thinking, and listen to and try to follow their peer’s thinking. (This was an ongoing goal all year and we’d made a lot of progress.)
So here’s what we did. Each person explained their strategy. While they did, I asked for volunteers to come up and record on paper what their colleague had done on our chart paper.

I stayed quiet while the person with the marker recorded, and then naturally turned to their colleagues and said, “Is this what you did?” or “What was your equation again?” We were getting somewhere.
In each group, someone had surprised me with their strategy. In the first group, J said she looked at her rectangle and thought, “Way too many to count.” So she folded her rectangle in half:

She thought, “Still too big,” and folded it in half again:

She looked at that and thought, “I can count that and then multiply by four.” The thing is, one of the factors was odd, so quartering led to a fractional result. She didn’t bat an eyelash:

She had a 7 x 10 rectangle, which yielded 70 squares. She then combined 6 half-squares to make 3, and had 1/2 left over. Each quarter had 73 1/2 squares. To figure out the total number of squares, she pinched together the 4 half-squares into 2 whole squares, multiplied 73 x 4 to get 292, and added them together to find 294 squares. She told us that the folding grew out of her comfort with sewing, and she was completely in command of her strategy.
I did the recording on J’s work. Not beautiful, but everyone agreed that what I drew matched what she did.

In the next section, L also began by folding her rectangle in half, but the other way:

Then she groused at me, “Oh, you made it not work out evenly!” A moment later, she said, “That’s OK, I love thirds.” Look how pretty:


A perfect square!

When she unfolded it, she had this:

Now we see one power of a tool. If I had explicitly asked them to solve the multiplication problem 21 x 14, I would have had almost all identical column multiplication solutions, which aren’t ripe for rich discussions. But this little graph paper rectangle yielded a wide range of approaches, including two strategies that made beautiful sense, visually, but had almost no chance of emerging if we’d only worked with numbers:
21 x 14 = 4 x (10.5 x 7) and
21 x 14 = 6 x (7 x 7)
Not only that, both J and L were in the spotlight for innovative math, when both J and L have historically not been so keen on the subject. They were the experts on these strategies, teaching me and the rest of their curious peers. If I could have bottled that moment and given it to them for safe keeping, I would have. It was a highlight of my year.
That brought us to the end of Tuesday. I knew I’d start with these on Thursday. Because J and L were in different sections, they hadn’t seen each other’s solutions, although word spread quickly throughout the staff and I heard them comparing notes after school (yeah baby). We began Thursday by marveling over the two strategies, comparing and contrasting the difference it made to want to avoid fractions or not be bothered by them. I then focused us on L’s strategy, written numerically. When we looked at the piece of paper, we could all see that there were six 7 x 7 squares. But when I wrote the equation:
21 x 14 = 6 x (7 x 7)
there was a lot of wondering about it. They all agreed that, if they’d been working with numbers only, they never ever would have transformed 21 x 14 into 6 x (7 x 7). They wondered, where did those numbers come from? Especially that 6? How could a 6 come out of 21 x 14? Eventually, there was recognition that 7 was a common factor of both 21 and 14. That insight led us to write:
21 x 14 = (3 x 7) x (2 x 7).
The 6 was in there somewhere, starting to become more visible, but this is a place where nobody was sure about the rules they’d learned once. What could you do with that 3 and 2? Add or multiply? Five or 6? We went back to the paper:

Do you see a 2 x 3 array there? A 2 x 3 array of 7 x 7 squares? Six 7 x 7 squares? Holy smokes, there it is. They saw where the 6 came from.
We played a little with the quartering strategy in the same way:
21 x 14 = (10.5 x 2) x ( 7 x 2) = (10.5 x 7) x 4
We wrote them up, talked some more about the associative property and what happens when you break factors up by multiplication. Now, to be clear, I am not saying everyone in the group would be able to recreate this logical flow independently yet. But I am saying everyone in the group was following along. They didn’t shut down at the formal math vocabulary, at the symbolic representation, at the diagram.
And that’s why I was glad to have a tool. In this case, the tool made it possible for everyone to access the mathematics here. It helped me gather a variety of solutions so we could make connections among them. It made tangible what had been abstract. It allowed my colleagues to bridge from something intuitive to something a little out of reach. And it made us talk with each other about the mathematics more, not less.
I’d call that added value.
I don’t get fussed over whether tools are high tech or low tech. I love and use them all. But I do take care to use them thoughtfully, not for the sake of using tools or tech, but for the sake of the mathematical learning and conversation they’ll allow me to engineer.
In early drafts of my book, there was a chapter called Mathematicians Use Tools. I was planning to get into all of this stuff. I cut it for the sake of length–it was already a huge book–and I thought tools had been written about a lot elsewhere. They have. I decided, instead, to showcase thoughtful use of tools throughout the book, which wasn’t hard because effective lessons often involved the strategic use of tools. Probably the right call.
There are times I regret not taking the deep dive into tools, though. I see so much tech-for-the-sake-of-tech, tools-for-the-sake-of-tools. I also see teachers still afraid to use tools for fear of mess or noise or lack of control or time or organization. I’d love to explore when and how and why we reach for them–or don’t.
Maybe this is the space.