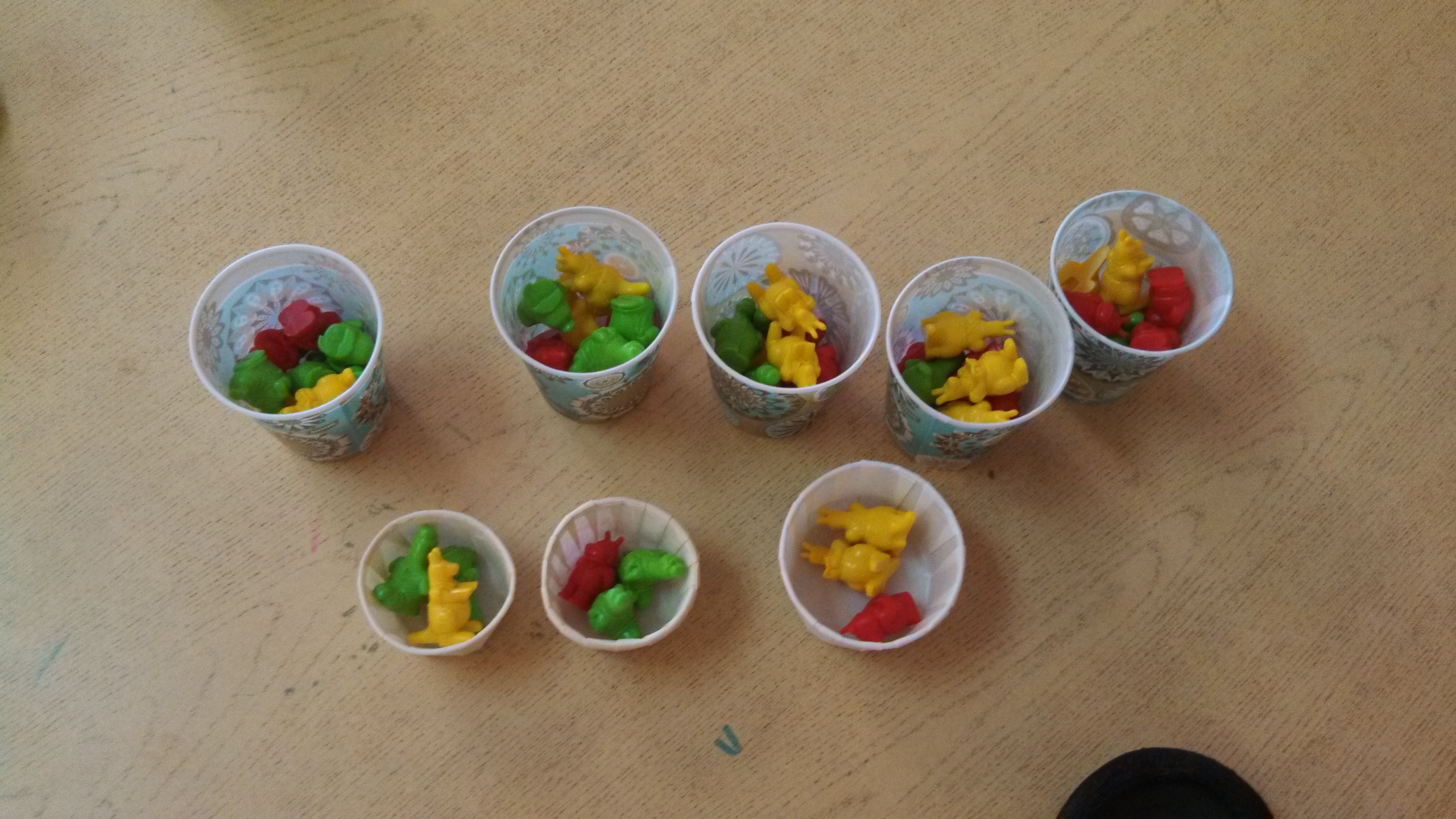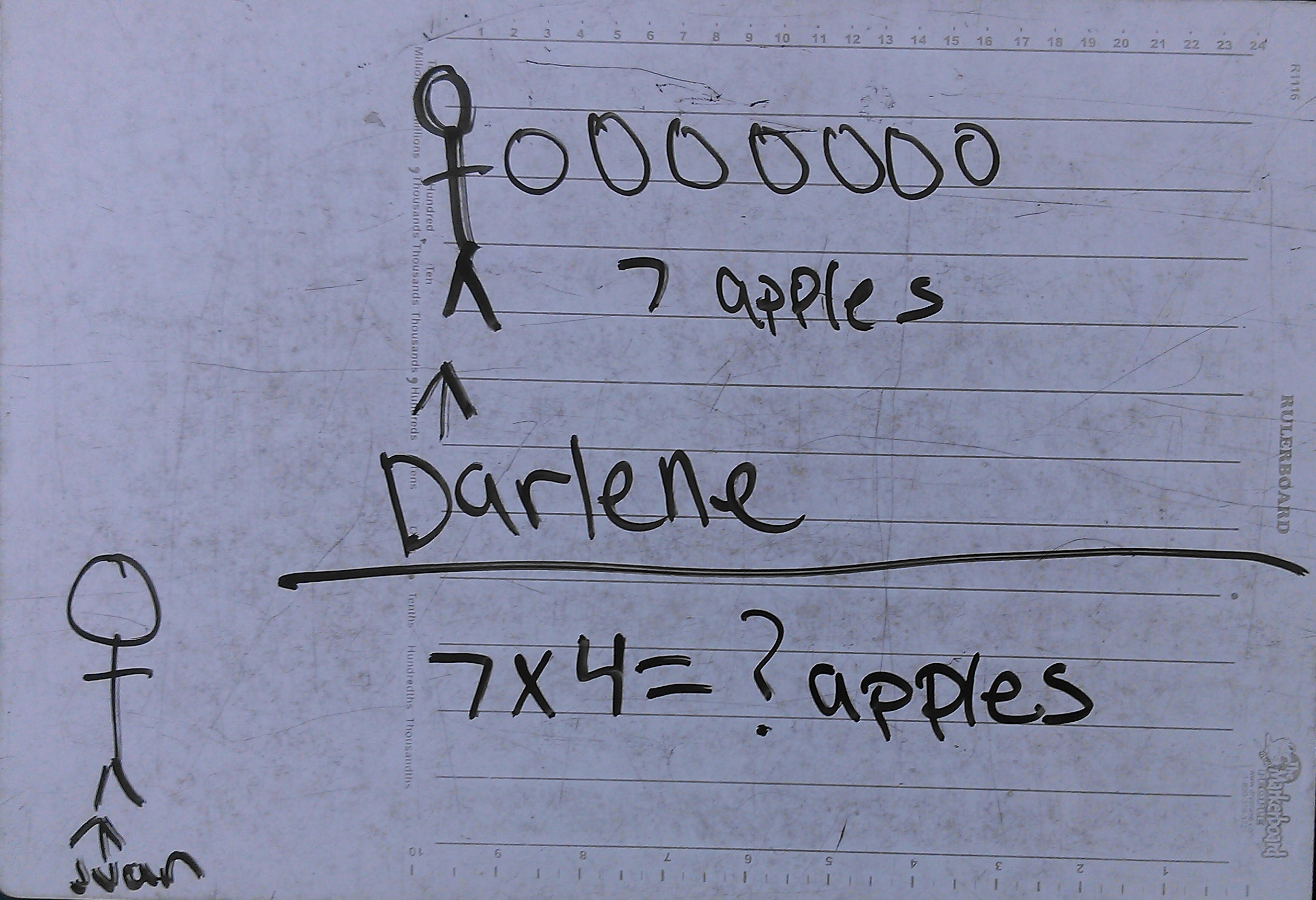I had a great time at the California Math Council (South) conference in Palm Springs a few weeks ago. I went to lots of super talks, but the two that have stayed with me the most were Ruth Parker’s and Megan Franke’s. I’m still mulling over both, and want to start by posting about Megan’s talk because it has made an immediate impact on my practice.
Megan discussed the relationship between children’s counting and children’s problem solving. She made a compelling argument against viewing them sequentially, or thinking that one is a prerequisite to the other, and instead talked about how they can develop in an intertwined, mutually reinforcing way. She argued that children can use what they know about counting to think about problem solving. And she argued strongly that children’s partial understandings about counting are incredibly valuable. Amen to that, sister. The CGI researchers have been leaders in focusing us on what students do know, rather than taking a deficit approach, and it was so gratifying to hear Megan make this argument in forceful terms, in person. I’m a total fan.
Megan showed several videos of students counting collections of objects (rocks, teddy bears, etc.) with partial understanding. For example:
- perhaps they organized what they counted and had one-to-one correspondence, but didn’t have cardinality, so they didn’t know the last number they said represented the quantity of the group. Or,
- perhaps they didn’t have one-to-one correspondence and didn’t count accurately, but knew their last number signified the total. Or,
- they had a lot of things going for them, but didn’t know the number sequence in the tweens (because they’re a nightmare and make no sense). And so on.
Megan showed a video in which a girl was counting a group of teddy bears (I think 15). She did pretty well in the lower numbers, but got lost as the numbers got bigger. The questioner then asked the student, “What if all the green bears walked away? How many bears would be left?” The girl giggled at the thought, collected up all the green bears, shoved them across the table, and counted the remaining 9 bears accurately.
My jaw dropped.
Megan made a powerful case that we can springboard off counting collections into problem solving, even if the counting is partial. She argued that students are already invested and engaged in the collection, so we might as well convert the opportunity. Some of her reasons:

I sat at my table thinking about how much work I’ve asked teachers to do. (If you don’t know what the counting collections routine looks like, take a peek at Stephanie’s kindergarten in this video:)
Teachers have gathered all these little objects, bagged them up, collected muffin tins and cups and plates, created representation sheets, taught the routine of counting collections. And yet, after the kids count and represent their collection, we just clean up.
It’s like we’re leaving players on base at the end of an inning. We’ve done all that work to get the hits and load the bases, but then we don’t bring them home. We don’t make full use of the opportunity we have designed. It was suddenly all so plain.
I tweeted about this idea of bouncing right from counting collections into problem solving, and my friend and colleague Debbie Nichols got the idea right away. She didn’t even wait for a counting collection. She started springboarding off an image-based number talk.
I visited yesterday, and Debbie’s K-1 kids were counting these cupcakes. They had all sorts of beautiful ways to count them.

- “I see two sixes, one on each side.”
- “I see four in each row, and there are three rows.”
- “I counted by ones. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.”
- “I counted by twos. 2, 4, 6, 8 10, 12.”
- “I counted by fours. 4, 8, 12.”

Students stood up and marked up the image on the smartboard, showing how they counted. They played with strategies to keep track and record. It was all great.
This is normally where we would have stopped, proud of ourselves for a worthy counting exploration. Not this time.
Debbie asked, “If we were going to write a story problem about this picture, what might we write?”
Arms went up right away. A student suggested, “Somebody had 12 cupcakes and took away 10. How many are left?”
Another student said, “Six cupcakes have raspberries. Two have rulers. Two have apples. Two have papers. How many are there altogether?”
Another student said, “I have 12 cupcakes. Evelyn gave me 10 more. Now I have 22.”
Debbie asked students to go get their notebooks and write a story. Solving it was optional.
Remember, this was a K-1. So, some kids who are very young K’s drew a picture and then talked about cupcakes:

Most kids were able to write a story problem and read it to us. And most of those kids wanted to solve it and were able to do so successfully:

One precocious student made the context a little silly so he could work with the kinds of numbers he likes. He explained to me how he found the answer of 450 cupcakes: “1000-500 would be 500, so another 50 more would leave 450”:

But my favorite conversation grew out of this piece of work:

I asked her how she’d figure out how many cupcakes she had now. She said, “I’d think 5 in my mind, and then come over to these cupcakes and start counting 6, 7, 8, 9…” A few minutes later, she told me, “It’s 40!”
After admiring her careful work, I said, “If I were going to count this, I would have thought 35 in my mind, and then come over to these cupcakes and counted 36, 37, 38, 39, 40.”
Now it was her turn to drop her jaw. She was so excited that we both found the same answer. I asked her if I could do that–can I switch the numbers around like that? I could literally see the gears turning and the wheels spinning. She is off to the races, starting to abstract and decontextualize and play with numbers.
I especially loved Debbie’s work because kids got to pose problems. We are way, way too stingy with opportunities for kids to pose problems. Most kids think math class is a place where the teacher asks questions or the book asks questions, and kids answer them. If we want students to understand that math is a way to ask and answer your own questions, we need to give them some chances to do the asking.
I hasten to add, during morning meeting, these same children were asking questions about infinity. “What’s half of infinity?” “What’s the biggest number?” “Is infinity a number?” Students who have their thinking honored–who are used to generating questions in math–will ask specific math-problem-type questions, but also large, important, relational, lofty questions. Problem-posing and question-asking in mathematics has a wide range. Kids need practice asking at all the different grain sizes.
Circling back to springboarding, today’s lesson drove home what Megan was saying. These kids had already spent 15 minutes studying these cupcakes, counting the cupcakes, listening to their classmates count the cupcakes. They were already invested, had thought about how they were organized, and were certain they were starting with 12. It hardly took any nudging at all to bounce them from their counting investigation to a problem-solving one. In fact, the two investigations were seamless.
My friends at different grade levels, can this idea transfer? When do you do loads of work, get students invested in a context, and then walk away too soon? I’d love to know.
In Debbie’s room yesterday, I kept thinking how lovely it was for students to see sensemaking as integral to counting and problem-solving, right from the start. How lovely it was for Deb to double the bangs for her bucks with this scenario. How lovely for her students to go deeper into a context that they could already visualize and understand.
Springboarding. I’m a fan.