Disclaimer: I do not work for any edtech companies and I have no desire to work for any edtech companies. I have no skin in this game. I make absolutely no money off any apps and plan on keeping it that way. This disclaimer means I have nothing to disclaim and you are getting my straight-up opinion here.
People often ask me what apps I can recommend for multiplication and division fact fluency. This question usually puts me in a tough position because, while eventual automaticity matters, I care about building conceptual understanding of these operations. My buddy Graham Fletcher recently described one path the progression of multiplication can take in this outstanding video. As Graham points, out, let’s not rush past all that great work!
And yet the requests come. This week, I fielded one from a teacher I needed to answer, so I threw the question out to twitter to see what’s new on the market. I’ve been looking around since, and the big money math fact app world is enough to send me into despair. It’s almost all awful. As I looked at them, I noticed I use three baseline criteria, and I’m unwilling to compromise on any of them:
- No time pressure. In some apps, there is a giant timer counting down. Or you have to answer before the sun sets. Or the context is such that the whole experience feels like an anxiety nightmare.
These screen shots came from the Arcademics game “Meteor Multiplication.” They’re basically embedding flash cards in the great Atari game of my youth, “Asteroids.” Except now, blasting asteroids isn’t fun. Now, if I can’t think of my facts fast enough while the meteors close in on me, I feel like I’ll be crushed to death. I know my facts. I found it hard to think when facing impending doom. This isn’t surprising. Studies like the one from Ashcraft and Moore have shown that:
“Overall, math anxiety causes an “affective drop,” a decline in performance when math is performed under timed, high-stakes conditions, both in laboratory tests as well as in educational settings. This means that math achievement and proficiency scores for math-anxious individuals are underestimates of true ability. The primary cognitive impact of math anxiety is on working memory, particularly problematic given the important role working memory plays in math performance.”
I don’t have math anxiety, but many of our students and teachers do, and timed drill is a leading cause. My 1st-grade daughter’s classmates told me they have stomachaches from the “Speed Round” in Addimals. Under no circumstances will I recommend any apps that involve time pressure or speed rounds. This criterion strikes the vast majority of apps because the premise of so many of them is that speed races are “fun.”

Source: http://www.arcademics.com/games/ - Conceptual Basis for the Operations. I don’t want to see naked number drills, especially not for 3rd graders. Flashcards embedded in silly or glitzy contexts are still flashcards. I want to see mathematical models like arrays, groups, hundreds charts, and number lines. Most of the apps put their money into developing exciting or humorous graphics to lure in customers, but what kind of mathematical sense does this make?
This screenshot is from SumDog’s Junk Pile, where the answers to math problems inexplicably turn into trash piled up in a junkyard. In this example, my correct answer to 80 – 10 turned into garbage. I mean, I’m trying not to be too sensitive here, but what kind of message does it send when we turn math into garbage? Literally! The first question I answered turned into a toilet bowl.
- Mistakes Must Be Handled Productively. The first thing I do when I trial a game is I make mistakes on purpose to see what will happen. The overwhelming majority of apps give some form of a Family-Feud-style giant red X. Sometimes with flames, molten lava, or puffs of smoke, because I guess the X is too subtle?

Source: http://www.specialeducationadvisor.com/wp-content/uploads/2012/05/next-dollar-up-3.jpg I’d estimate that, 9 times out of 10, most apps just move to the next problem after a mistake. The kids don’t get to figure out where they went wrong, don’t get to learn from the mistake, and don’t get to try again. Talk about missed opportunities. And then there’s the way mistakes affect scores and the endless parade of stickers, stars, and tokens in these games.


Source: http://www.arcademics.com/games/tractor-multiplication/tractor-multiplication.html In this game, we played tug-of-war in tractors, because I guess that’s a thing. Anyway, it was a race. In the second round, we did some tandem tractoring where I was partnered with a stranger on the internet and we raced two computers. I was Player977, and I answered 35 questions/minute. That’s a much faster rate than we can ever expect students to recall facts, even with automaticity. I made one mistake on purpose and guess what? We lost. I can’t tell if I lost because of the one mistake, or I lost because my internet-anonymous partner, Player807, needed a little more time to answer. Am I supposed to think of Player807 as deadweight? I mean, come on. However I slice it, I lost through some algorithm that only counts speed and correct answers and discounts mistakes as bad. Little surprise that most of these app web pages have correct answer counters, like McDonald’s does for burgers.

So what apps can I recommend? The list is painfully short. One program rises right to the top. Dreambox is my preferred app, without a doubt, by a mile, far and away from the others. Students have plenty of time to think. Cathy Fosnot’s landscapes are built right into the structure of the app, so students are often working on a variety of interrelated ideas and models. For example, Daphne is in 1st grade, and she’s working with rekenreks, number lines, and tens frames.
The modeling is just off the hook. I took these screenshots while Maya (3rd grade) was working in a context for place value. She needed to think of 4 different ways to pack 703 objects among cases of 100, boxes of 10, and loose 1s.
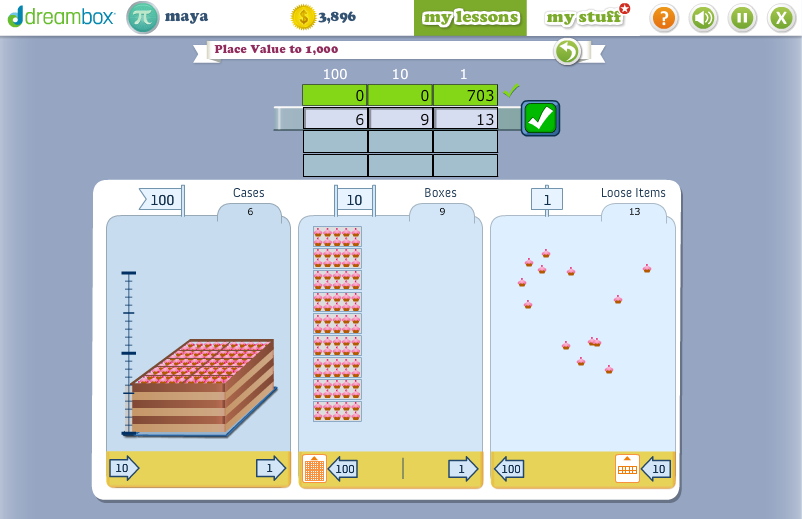
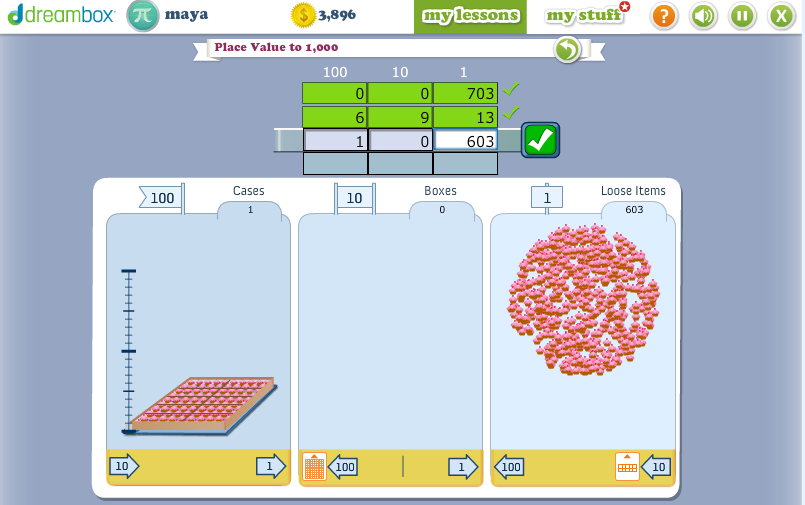
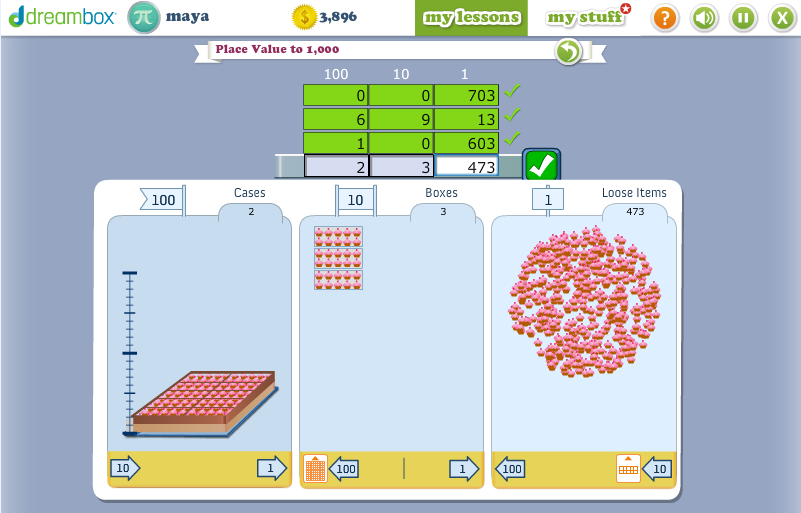
Given the poor conceptual underpinning of my kids’ curriculum, I sprang for dreambox at home, so I get to peek over Maya and Daphne’s shoulders now and then as they play. When they make a mistake, the response is, “Oops. Something doesn’t seem quite right.” The kids are expected to try again. If they’re stumped, the app supplies really good support, layered in like a teacher would.
This is straight talk. My kids love dreambox and ask to play regularly. I’m down with it because, on top of it nailing all three of my criteria, the story contexts are fun – pirate ships, dinosaur fossil excavations, amusement parks – and the messaging about math is aces from both equity and growth mindset vantage points.
What else is out there? I’ve heard good things about Wuzzit Trouble from Keith Devlin. I haven’t tried it myself, though. I plan on giving it a go.
h/ts to John Golden and Paula Krieg for pointing me toward Bunny Times this week: It’s actually free. It isn’t as glitzy as the other apps and doesn’t produce teacher reports or have a dashboard. It’s also focused singularly on multiplication using arrays. But, my friends, the math is right.

They build in some nice decomposition work as the problems get bigger, so kids start to build foundational understanding of the distributive property.

Over time, a fog rolls in, which discourages counting by ones.

And check this out. Look what happens when you make a mistake.

You see that feedback? See that carrot there? And do you see that lovely sign, right in the foreground? The one that says, “TRY AGAIN?” So we did.

I wondered what Maya would think of this app. She adored it, and I watched her do some really good thinking. For example, she’s still a big fan of doubling. At the beginning of her bunny time, she’d think about a problem like 8 x 12 as 2 x 12 = 24, 24 x 2 = 48, 48 x 2 = 96. After some time with the bunnies, I saw her solve 8 x 12 with (8 x 10) + (8 x 2). That’s a nice development. She started thinking strategically about breaking the dimensions into smaller numbers, using more 5s and 10s and place value-based thinking.
So, I was saved from my despair by the lovely design at dreambox and the solid math of the bunnies.
My message to most app makers? Try again.
Clarification, Jan 5 2016.
I think I need to clear something up. Dreambox and the Bunny Times aren’t comparable. Dreambox is a full program. Soup to nuts, as they say, A huge K-8 progression, thoughtfully organized and designed, that develops both understanding AND fluency, together. That’s why I like it so much. And, I’m sorry to say, that’s why its pricepoint is much higher.
The Bunny Times has nothing like the scope or scale of dreambox. It’s not trying to be more than it is. It’s an app tightly focused on one part of developing multiplication. But when they decided how to structure it, I think they did a nice job thinking it through.
And they met my criteria of no time pressure, a conceptual basis, and handling mistakes productively.
I personally think that’s not a high bar. I mean, those three criteria are my bare minimum. That’s why it’s stunning that so few apps clear it.
People have been tossing apps my way all day both on twitter and in the comments. I’m happy to take a look. But I’m telling you right now, if it has time pressure, no emphasis on understanding, or poor handling of mistakes, it gets a fail from me.
Clarification #2 Jan 7 2016
Looking through comments and twitter conversation about this blog, it seems there are two things I didn’t make nearly clear enough.
- This list is not exhaustive. I certainly didn’t try everything out there. I shared dreamBox and Bunny Times as two examples at two price points and two scopes that meet the criteria I outlined. And I shared that I’ve purchased dreamBox at home because I think it’s great.
- Lots of people have been asking about other factors and attributes about games, apps, subscriptions, programs, etc. This is a great question and the main thing I want to clarify. There are lots of other characteristics I look for when evaluating games and apps. Here’s a partial list, the best brain dump I could do before caffeine this morning:
Is the game engaging? Do kids like it? Are they motivated to use it? Does it encourage students to interact with each other? Does it help build mathematical intuition and sense-making through things like prediction, estimation, revision, reflection? Do students get multiple iterations to solve until they decide they’re satisfied and pleased? Does it reduce barriers to entry? Does it break down or contribute to stereotypes about who can and can’t do math (students of color, multilingual students, students with disabilities, gender)? Is the mathematics it addresses important? Does it contribute to societal myths about what mathematics is, or unseat them? Does it adapt to students’ performance? Does it yield useful formative assessment for teachers (not just “data”)? Do the problems have any openness (beginning, middle, end) or is it all answer-getting? Do students get to write? Are there options for student creativity and initiative? How are the graphics? Is there mathematical beauty and delight? Do the kids ever get to choose among representations and models or create representations and models themselves, or is everything provided? Do the kids decide their strategy or do they execute what the program chooses? Does it portray mathematics as inherently interesting, or something that needs to be dressed up in gimmicks and rewards?
If you’re wondering what program could possibly do all that well, I’ll send you to teacher.desmos.com. Have a look around. Enjoy.
But here’s the deal. In this particular blog, I wasn’t trying to list all the things I consider. I was trying to give my 3 non-negotiables. As I said above, I won’t compromise on any of them. I don’t actually care how great the graphics are, how good the teacher reports are, or how many people tell me “but kids like it!” if the program has time pressure, no conceptual basis, and handles mistakes negatively.
That’s what I meant by baseline criteria. If an app meets those three criteria, then I’ll look at the rest. But when I first look at an app, these are my three questions:
- Is there time pressure?
- Is it conceptual?
- How does it handle mistakes?
Update July 11 2016
Thanks to Julie Wright and Dan Meyer for recommending Sumaze! Super strong. Thumbs up. And free!





Some enhancements to these two would be the opportunity for the user to create their own problems, and interact more with the program (app). I need a fresh project !
Oh, to be clear, there is always room for improvement. I’m talking about finding things that meet my bare minimum requirements. Turns out to be surprisingly hard.
I found Woot Math for fractions. It adjusts “instruction” (or maybe it’s better termed problem sets?) to student work and I loved the way my kid was talking to herself while she worked each new problem. It has multiple representations for fractions and challenges students to use the one that make the most sense to them, and sometimes limits the representations to highlight certain aspects of the math.
My only complaint has been that my daughter gets really caught up in getting all 3 stars for each new chapter — it was needless, and she’s noticed that sometimes she didn’t get them which either throws her into despair or motivates her to do that whole chapter over so she can collect all three. I also don’t like that you only get two chances to get the bonus problems “right” — my kid really, really wanted to work through the more challenging problem solving context. I shared this feedback with the Woot Math people at their booth at NCTM Nashville. Not sure if they will or have taken that feedback to heart.
Interesting. Haven’t seen it yet. I’ll check it out! Did she ever play Refraction? https://www.brainpop.com/games/refraction/
It’s free for this school year.
Also, is there some way to get a sense of where things are going with the math in the refraction game? Or, can you tell me more about the content?
Great work, Tracy! Thank you for sharing! I need to search out great/acceptable apps for K-2. Let me know if you have any recommendations.
Thanks, Jamie!
I have found that BrainPop has THE BEST games. They seem to have set their benchmark really high when it comes to conceptual development, flexibility, and trial and error. Plus, their assortment and depth of videos rocks too!
Nice. I’ll check them out more. I like Refraction already.
Great post! However, my two cents here is that there is a distinction between facts based skill apps (which still have a place) and apps that are more conceptual and use models like dreambox. There are also other factors like cost (is the app free?) and what kind of data can be accessed by the teacher. It would be great to gather a list of desirable features for apps in general and then rate them based on these features. And the toilet bowl in junk pile (Sumdog app) is hilarious to students.
Thanks, Eric. There are lots of factors that could be considered. Engagement, graphics and design, whether students interact with each other, whether the teacher gets useful formative assessment, whether the program adapts, etc. And I do consider all those factors when thinking about which apps and programs are really fantastic. This is where desmos is charting all kinds of new territory. Amazing.
In this post, I purposely didn’t consider any of those factors. I wrote about the bare minimum: my three non-negotiables. Making the app free or funny can’t outweigh a non-negotiable.
I’d prefer the *option* of timed practice. Mathisfun.com has training that gives you the option, tho’ if I remember right, it’s strictly drill w/0 the illustrations.
Dreambox was the first and best in math software that actually, no really! included visual and conceptual content. THey let me test drive it w/ some of my students, but are only interested in K-12 scenarios; since we couldn’t purchase things the same way, that ended that conversation.
Huh. That hasn’t been my experience with them.
It was my experience. Now, this was several years ago. In the college setting, we need students to be able to use financial aid to get access to the materials. The fellow I was working with said he’d asked but … they were only able to do things directly (as they do with parental orders) or as class sized purchase orders.
I would love to adapt their stuff to be a *little* less cute for our adult students who are sometimes sensitive (but lots less nowadays since so many online games are ‘cute’). I’d also like to work more gradual bridges from visual/concrete to symbolic and linguistic. As with Dragon Box, I see students able to imitate the visual patterns and get things right, without making the connections to (shudder) math problems.
I highly suggest the Dragon Box apps. They are great. I am most familiar with the Algebra ones but have heard really good things about the others as well.
I keep hearing that. I haven’t ever played them. I was just poking around and have to admit I wasn’t super excited by the ad: “Kids don’t even know they’re doing math!”
If you’re looking for kids (3 year olds) to start recognizing numbers, my son loves Endless Numbers (and it’s companion Endless Alphabet). http://www.originatorkids.com/?p=731
Seconded for DragonBox Algebra 12+. We’ll be using it in an AIS setting for our Algebra students.
End of product placement.
I love Dragon Box as well. My 12 year old completed all the levels already (wish there were more!) and even my 5 year old can do the first few levels, which is gearing him towards algebraic reasoning for later
Yeah, I keep hearing that. I will check it out. It feels a little trick-ish though, no?
Thanks, Dan. Will try them!
I’ll be the first to admit that OpenEd’s Common Core Quest could use work on “interface” for younger kids, but the feedback loop is very good. Rationale of why what students chose was wrong in student-friendly language and a video or game matched to the misunderstanding. Then they’re given a chance to try again or skip it, all of which goes to the teacher in a chart. Basically was a teacher using OpenEd a lot and kept giving them feedback how to make it better so they hired me last year… (I am lead content curator mainly for math and science – checking videos alignment to standards and working on expanding the minutia of the skills in those standards). Feedback here or to brandon@opened.com is great either way!
That’s huge. Feedback loop is huge! I’ll try to check it out. Thanks, Brandon!
Disclaimer: I trust teachers. I do work for many edtech companies and I have no desire to make money off any apps and plan on keeping it that way. This disclaimer means I have a lot of experience playing with interactive learning tools and you are getting my straight-up opinion here.
Thanks Tracy for your feedback on fact-based apps. I agree with much of this. It may be that some personalities enjoy time pressure – but in general it is not a good idea to make this a required feature for a learning tool. I agree that we need strong contexts to embed conceptual understanding within games (intrinsic integration of game and learning mechanics). Your third point is the biggest point I make in my work as educator in residence for edtech companies. Immediate constructive feedback that allows a player to reflect and improve without intervention is what makes a great video game experience, as well as a great learning experience.
I think many great products were suggested in the comments, but here are a few more.
Duolingo is excellent.
Desmos is transforming math education.
Dreambox does make good learning tools.
Dragonbox won the internet in 2014.
Lab4U is putting lab experiments on student mobile devices.
Slice Fractions and Refraction are the best things that have happened to fraction education since Jaime Escalante brought the butcher knife to class in Stand and Deliver.
GlassLabGames is the Steam of educational games.
Graphite is the Google of educational tools.
code.org and the Hour of Code has made algorithmic literacy a educational policy point.
Much more to say – and I would love to get connected to any communities who love discussing these points.
Love and light,
Evan
Great resources to check out, thank you!
Love Slice Fractions and was happy to see someone mention it here. I’ve enjoyed watching the conceptual thinking of my 5 and 7 year old daughters as they played it on two cross-country flights at Christmas.
THANK YOU! I LOVE that you address this issue! Self-confession: I USED to be a timed math fact teacher. I stopped because I saw the anxiety it was causing and I never noticed a true increase in fluency.
I am fully aware of the “math wars”…not just with teachers, parents, the pro/anti Common Core advocates, but also with researchers. Students need fluency. Absolutely. They also need conceptual understanding. It’s not either/or; it’s both. I think of it like learning a foreign language: I can memorize verb endings and conjugations; I can spit them out by looking at flash cards; I can even do this (breaking out in a sweat) under timed conditions. Knowing the conjugated verbs absolutely decreases my cognitive load. That does not mean I know what the verb means, nor does it mean I can use this verb correctly, fluently in sentences in genuine conversation.
An additional problem is there ARE a few research studies reporting that students performed better when under a time limit. The real issue is that the implementation of these drills did not occur in the same way I have seen anyone give timed fact tests: researcher sitting across from student using flash cards, or similar. My experience with timed drills (my own horrific past practice and that of colleagues) is using either web-based programs (or apps) like you mentioned, or a worksheet with an absolutely unreal number of facts (visually overwhelming) and a timer of 1-5 minutes…or something like that. Students HATE THESE!!! The anxiety is real. Fluency comes with practice. Not the drill and kill kind. Every single skill we acquire requires practice: tennis players practice different strokes, playing a piano well requires playing scales…discrete skills need practice. Timed fact drills are not the only way to practice. NO CHILD IN FIRST OR SECOND GRADE SHOULD HAVE HAD ENOUGH NEGATIVE EXPERIENCE IN MATH TO HAVE MATH ANXIETY! That is exactly what I have seen! That is evil.
For what it’s worth, I am becoming sort of an adaptive/mastery evangelist. I believe that if a student is going to spend the time on practice then I prefer software that will level up and down based on their progression. I found a service that reviews apps (though not web-based software) based on very specific learning metrics. http://www.balefirelabs.com —They are my “go to” because I can see at a glance whether or not an app is adaptive, whether it provides feedback, etc. Sometimes I even use an app that hasn’t received their highest rating…usually because the device I use doesn’t support a particular type of software, or because the app didn’t have a teacher dashboard…something like that. Either way, with their metrics I can see WHY an app received a specific rating. I did look up the apps you recommended and the ones you did not like. I did not see ratings on these. I am guessing because Dreambox is a subscription and the others are websites? I’m not sure.
Anyway…THANK YOU for this post!
Thanks so much, Rene. Totally with you on anxiety and timed tests. I’ll check out balefirelabs!
@ “I am fully aware…. …. genuine conversation.” You need and should to adjust “everything” in learning to Van Hiele levels of learning.
http://www.provengrupa.com
Thanks for these two recommendations. I’m frustrated by the online maths games my son’s school subscribes to – not only is the maths done under timed conditions, which makes us both anxious, but the ‘reward’ for getting ‘enough’ answers correct is usually a short time playing a game that he finds equally frustrating. The most recent ‘reward’ game was a chance to aim a ball at a football goal which meant that when he missed this, which happened frequently as it seemed to be pure chance, he was upset and frustrated even though he’d done the maths question correctly!!! Urgh!
Jemma, that sounds awful and makes me really mad, especially because the app developer made quite a bit of money creating that. So sorry.
While I think your 3 criteria are excellent gate-keepers, there is a type of game/activity that doesn’t have an embedded conceptual model, but also isn’t flash cards which I would let into the party. Two examples are Sequences and NCTM Times Square (free, but log-in to Calculation Nationrequired).
In these activities, calculation is inherent to the play, but it is not the objective. The objective is to … well, win or get as many points as possible. Alongside that, there are a huge number of notice/wonder questions that (can) come up related to the structure of the game and strategies for play. Also, mistakes made in play have logical (within game) consequences that are neither trivial (within game) nor overblown.
Because these don’t embed a conceptual model, they aren’t useful for teaching students what multiplication is or strategies for computation, but I think they are a great next (mathematically rich) step after those foundations are in place. And, for the lovers of fluency: in a typical 20 minutes playing sequences, I probably do 300-500 calculations (mix of addition, subtraction, multiplication and division). Students, of course, will be slower and do fewer calcs, but still a lot.
Thanks, Joshua. I think lots of games fall into this category. Greg Tang’s stuff, KenKen, etc. The goal seems to be a kind of nimbleness with numbers. If kids already have a solid conceptual basis, OK. But how often does that happen class-wide?
Got excited because I’ve never heard of Greg Tang. After a couple minutes, I’ve now test played his free ones and not sure I will use them. Maybe I’ll have my kids at home try them out and see how they react.
Theoretically, I think it is desirable to have kids encounter some uses even before they have a full conceptual understanding. In the recent words of Piper Harron: “you are allowed to use math you don’t yet understand.” I’ve personally found some mix of activities the focus on developing/strengthening conceptual understanding and then applications to be effective for me and our students. However, I only propose opening the door to activities that are mathematically interesting in their own right.
Also, live, in-person (as opposed to electronically) we use puzzles and games as a complement to model-based (including manipulative-based) calculation strategies. Said in a less pompous way: we play a bunch of games and when a kid is stuck on some calculation, we prompt and help them use tools to do the calculation. This (usually) happens after they have been shown the models and tools, though occasionally we jump the gun and introduce a new model they haven’t seen. When that happens, we usually find the kid is super receptive, but I don’t think it is the best time for them to really absorb the new perspective.
Tracy, I think you are pretty much on target. As the founder of an edtech company, i constantly struggle to ensure that our designs are first and foremost, educationally sound. The graphics and audio should be engaging to students but not distracting or confusing. Ideally, the graphics and audio will reinforce memory and understanding of the key concepts, not distract from it. It helps that I spent a decade in the video game industry first where I developed Playstation games. Oddly, I had the same struggle there. Our games were fun because of the gameplay with the graphics and audio designed to enhance the experience. We were against gee whiz graphics that got in the way of gameplay.
Here’s a simple example of one of our phonological awareness learning activities which has some game-like elements.
http://www.spellingcity.com/which-initial-sound-game.html?listId=18535413
Interesting, thanks! You might enjoy Dan Meyer’s outstanding talk: http://blog.mrmeyer.com/2014/video-games-making-math-more-like-things-students-like/
I’ll take a peek at your games as soon as I can.
I love your two recommendations, thank you!
I wanted to ask you specifically about Khan Academy. I use it extensively with my high school students and occasionally with my six year old daughter. I believe it meets all of your critical requirements. It is free like Bunny Times and even more comprehensive than Dreambox, going all the way from Kindergarten through a decent amount of college+ level math and includes topics outside math as well. I do not think it is ideal but I really think the philosophy is pretty reasonable and the vision for the use of Khan Academy matches my own. I use for a high school Algebra 2 class in place of 50% of my paper homework. It is excellent for developing fluency and supports a classroom approach with a focus on conceptual understanding and modeling.
Thanks! I’d love to know how Khan Academy supports conceptual understanding and modeling?
It’s improved a lot since those first lessons and a lot of conceptual explanations have been added, so it is useful for supporting a good teacher. It still (from what I’ve seen browsing) does leaps and bounds (so “interesting exceptions” are almost always infused too early IMHO)… and I still find “little” mistakes like calling a multiplication problem a sum. (I think the video where he said 2 x itself was the same as 2 x 1 has been moved…)
I still wouldn’t wish it on my students
Thanks for asking!
I believe that the primary value of Khan Academy, and fact-based apps in general, is in supplementing instruction as opposed to replacing instruction. I don’t use Khan Academy to develop conceptual understanding. Instead, I use it as a space for students to solidify their conceptual understanding. I assign approximately one quiz per class period worth of new material. These quizzes are completed by students on their own schedule. The quizzes are selected to match up with the concepts that we tackle in class. I have written a more detailed description of how I use Khan Academy because I have been asked to defend its use in the past and I believe it greatly improves the quality of learning in my classroom. Approximately 20% of the quizzes I assign are designed to focus on conceptual understanding. The other 80% are primarily assigned because they allow students to develop fluency without undermining the math practices I try to reinforce.
I know you are approaching this from an Elementary context. Unfortunately, I have limited exposure to elementary so I am going to offer up a couple quizzes from high school that illustrate conceptual understanding:
Shift and Scale Parabolas
Summary: Transforming Functions
I give students space to develop a conception of vertex form for quadratics as a capturing of translations and dilations of y=x^2. The in-class work here is significant in terms of deepening student understanding of a function, of transformations in general and of looking for and making use of structure. The content is very cognitively demanding and most students need a lot of practice to be able to develop the appropriate number sense and abstract reasoning. I believe that these two quizzes support that sense.
Whoops, one of my links was bad. Here is the corrected link for the Shift and Scale Parabolas Khan Academy skill practice.
Very interesting read. Admittedly, I am reading this with my parent hat on more than my educator hat on and I will be trying these out with my son. I like the way you break it down.
It does make me wonder though how different groups would prioritize the various criteria you listed (and which others including Eric Milou) added to. For example, would a game that meets your criteria but is boring be more productive than one that is entertaining but has a timer. It would be lovely to have a more comprehensive database since it is so time consuming to do what you did.
Thanks for sharing!
Thanks, Robert! I replied to Eric above.
Thanks for the great recommendations. Do you have an opinion on MobyMax?
Never played it. Does it pass all three baseline criteria?
Your baseline criteria of…
Is there time pressure?
Is it conceptual?
How does it handle mistakes?
got me thinking about how your criteria for apps can be used as criteria for someone to examine their own teaching style. .
The most interesting model l ‘ve seen for dealing with “handling mistakes” was at Mike Lawlers’s math page, https://mikesmathpage.wordpress.com/2015/12/08/christopher-danielsons-intermediate-value-theorem-activity-with-younger-kids/ showing a Christopher Danielson’s Desmos activity.. The student answers the question, sees how other people have answered the same question, gets a chance to reevaluate their answer then discovers the solution. There is never a moment where the student is WRONG, rather it’s a process of thinking and discovery. Very cool. Part of my take away from your post is that there are as many styles of apps as there are of teaching, and teachers will likely choose the ones that are extensions of their own teaching philosophies.
The other take away is that it appears that the best way to get a whole lot of app recommendations is to write a post about a few of them.
True story, Paula. I wish I had time to look at them all!
Thought-provoking read. As a parent and as a teacher, I agree with your #1 non-negotiable. At CMC in Palm Springs, Jo Boaler was an opponent of speed also.
Jo has been great about addressing speed drills. I’m grateful for her leadership on it.
I have a game on my phone. I just played it and thought of your post. I can’t find it online, sadly. It seems to be called 1 Whole. There are rectangular shapes that fill with liquid. You push one toward another and they go together if the sum is less than or equal to one. You watch the liquid rise. If it’s 1, it goes away and you get points. You keep going until the screen is full of things that won’t combine (sum > 1). There is no time pressure, the conceptual basis seems strong to me, and mistakes aren’t allowed. No penalties, no bad sounds, it just won’t work. I think it’s pretty good. I wish I could find it online.
Coming late to the game here, but check out Math Doodles. It hasn’t been updated in awhile, but does have a lot going for it. First, it presents playing with math as fun in and of itself. It lets you choose a lot of things to adapt the game, including the way numbers are presented–including as digits, words, dice, even ten-frames. Lots of good stuff in this one.
I’ve heard Math Doodles recommended by several people. I will definitely check it out. Thanks!
Have you looked at ST Math? It is a supplemental math program, but can be used on iPads. Licenses have to be purchased, but I think you might be nicely surprised by this program.
Thanks, I’ll check it out!
In my first year of teaching, I did a unit of work where students had to play a wide range of division maths games online and evaluate them. I asked them to consider how these games helped them learn division facts. The students were enthusiastic about the project (our teacher is letting us play maths games in class!) We all came to the conclusion that to play the fluency games successfully, you needed to know the maths first.
In my second year of teaching (before iPads) I was involved in trialling the Nintendo DS game, “Brain Training.” Students were given a series of simple facts across all four operations to answer as quickly as possible. We did it for 5 mins everyday with the goal of improving fluency.
At the beginning of the year we did a timed pretest on paper. We did the same pencil and paper test at the end of the year. When I analysed the results, I discovered that while students could answer the test twice as fast (or better), they did not improve their scores. In fact, they made the same errors at the end of the year that they made at the beginning of the year! The following year we had to participate again but this time I made a change: the first time students made a mistake, they had to close the lid (stopping the timer) and write it down in a special journal. Then they could finish the session. At the end of the session, they had to figure out the correct answer and write out the whole equation three more times. I would mark this, and look for trends across the class and for individuals, that could then inform my teaching. I think I was still focussed on having students find ways of remembering quickly rather than developing conceptual understanding.
Shortly after I went to a primary (elementary) maths conference where an accademic presented a session on maths apps. One of her comments resonated with me: it’s not necessarily the app, but how you use it that determines its value as a tool for teaching mathematics. For example, she described a small group of students she had observed using a fluency app. Four students played while a fifth looked on with a clipboard. The role of the fifth student was to notice which questions were proving tricky for her classmates. At the end of their practice time, the students met with the teacher. The observer reported back to the group and they discussed these tricky questions: what about them was tricky, what they had been thinking at the time, how others had calculated the right answer. They pulled out maths materials and explored how they might use them to find the answer. Then they had time to record ideas in their maths journal.
In summary, IMHO:
* time pressure has some value at improving fluency for known facts
* the best error handling and development of conceptual awareness should come before and after students play fluency games – in learning experiences where students talk about ideas with each other and their teacher.
This is a fascinating comment. Thank you!
Tracy, your criteria are spot on and it’s nice to see them in virtual print. I’ve read and re-read this post and each time (with every clarification!) it resonates more because your “bare-minimum” is an expectation of research-based, best practice when it comes to building computational fluency. There are way too many apps out there that don’t meet these criteria. My hope moving forward is that math app developers will read your post as many times as necessary to change the way they think about what math apps should do. I’ll be tweeting this out to get the ball rolling on this.
I also plan to share your three criteria with grant recipients all over GA looking for guidance on math tech in mid-February. Thanks so much for this. Well done!
Thanks, Mike! Always happy to think things through with you. Glad this one was helpful.
I see this (Teach Your Child) Android free math app for children helpful and quite complete:
https://play.google.com/store/apps/details?id=com.apricot.tyc_math
Thanks for this list! My 6th grade students students love SumDog. I sometimes use computer lab time to reward them with a period of SumDog. They don’t think of it as Math work at all!
Hi,
I have produced a times tables app based on using the visual patterns produced on a 100 square. It meets your criteria in so far as there is no time pressure and it is conceptually based. I had not dealt with ‘mistakes’ other than with color coding and light hearted audio feedback as I regard ‘mistakes’ as attempts. I would however appreciate any feedback on dealing with these mistakes. I am considering extending the functionality of the app but I don’t want to overload learners with superfluous features.
Thanks in advance for any interaction with Get It Times Tables.
Karl
https://play.google.com/store/apps/details?id=com.silverbrock.getittimestables
Hello! This post was recommended for The Best of the Math Teacher Blogs 2016: a collection of people’s favorite blog posts of the year. We would like to publish an edited volume of the posts at the end of the year and use the money raised toward a scholarship for TMC. Please let us know by responding via http://goo.gl/forms/LLURZ4GOsQ whether or not you grant us permission to include your post. Thank you, Tina and Lani.
Math Mountains Add & Subtract is free – it’s not glitzy, and meets your criteria. They also have a Multiplication & Division app for 99 cents. https://itunes.apple.com/us/app/math-mountains-add-subtract/id1168485242?mt=8