Last week I was hanging out in a kindergarten during Counting Collections. It was amazing and beautiful. Afterwards, the kindergarten teacher, Becky Wright, and I were talking about the challenge of switching from counting by tens to counting by ones. These three students will give you a sense of what happens at the transition.

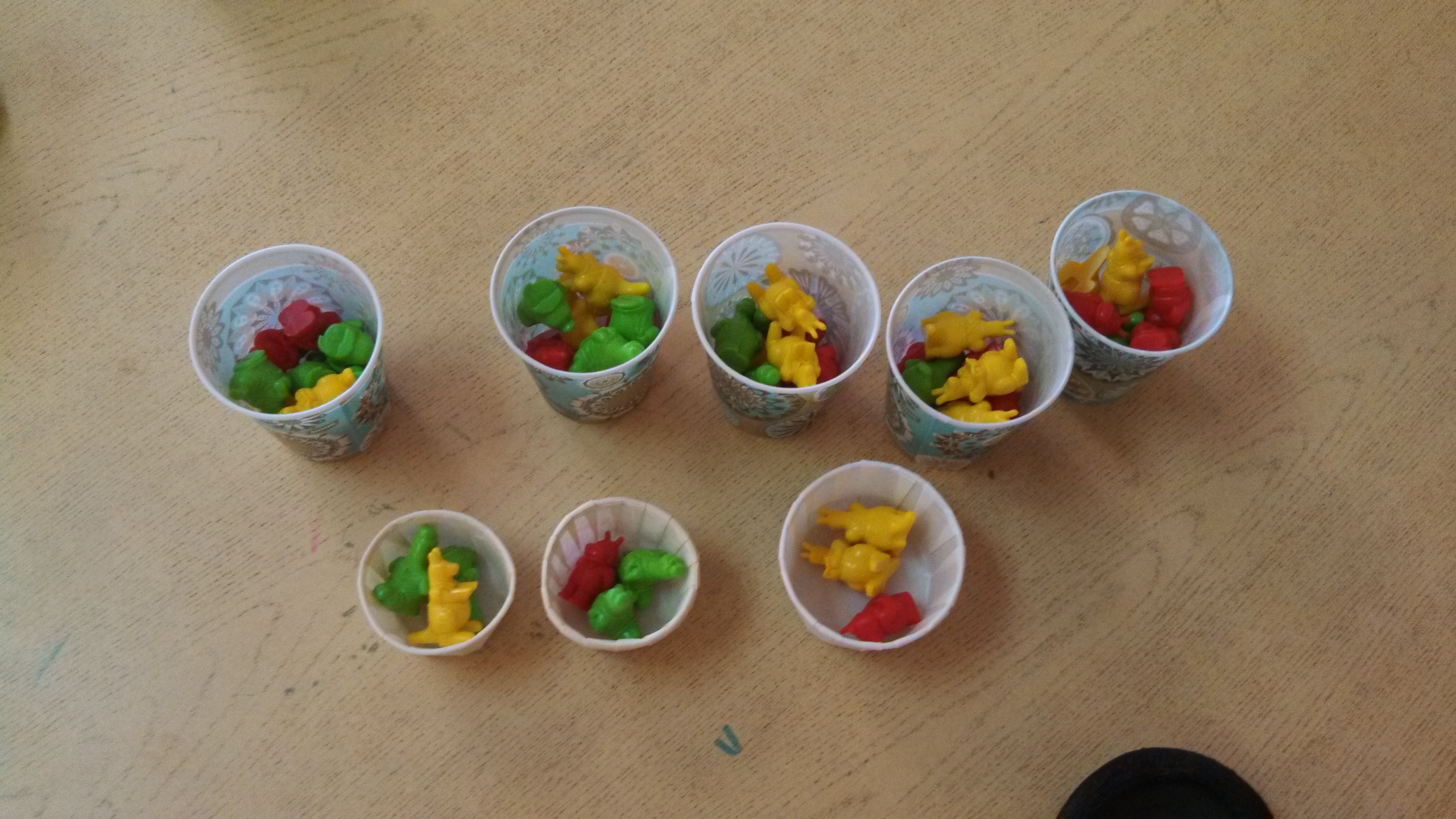

We’ve all been thinking about what might help students get more comfortable switching back and forth between counting by tens and counting by ones. Today, Becky and I were talking with Debbie Nichols, who teaches 1st and 2nd grade. Together, we landed on the idea of passing out 10s and 1s – connected sticks of ten cubes and single cubes, base 10 rods and units, etc. – and then having a counting circle.
In kindergarten in the late fall/winter, Becky would have the kids holding tens positioned at the beginning of the circle. As kids counted around, adding what they have, they’d keep a running total of the cubes. So a count with 20 kids might sound like “10, 20, 30, 40, 50, 60, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83” if the first 7 kids were holding 10s and the rest had 1s.
What about having one of the kids with tens switch places with one of the kids with ones? Now the count might be, “10, 20, 30, 40, 41, 51, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 81, 82, 83.” Ooh!
Or, what about going around the other way, starting with the ones and ending with the tens? “1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 23, 33, 43, 53, 63, 73, 83.” Hard!
With 1st and 2nd graders, Debbie wanted to pass out tens and ones at random. Her kids came back from recess and we gave it a go right away:

As kids counted around, Debbie kept track by pointing on the hundreds chart. After one count around, we found we had 77 cubes.

The kids asked if we could count around the other way – counterclockwise instead of clockwise – and we had a great discussion about whether we would still land on 77 or not. I suggested Deb keep track of the running total by tracing its path on the hundreds chart, using a different color for each count:
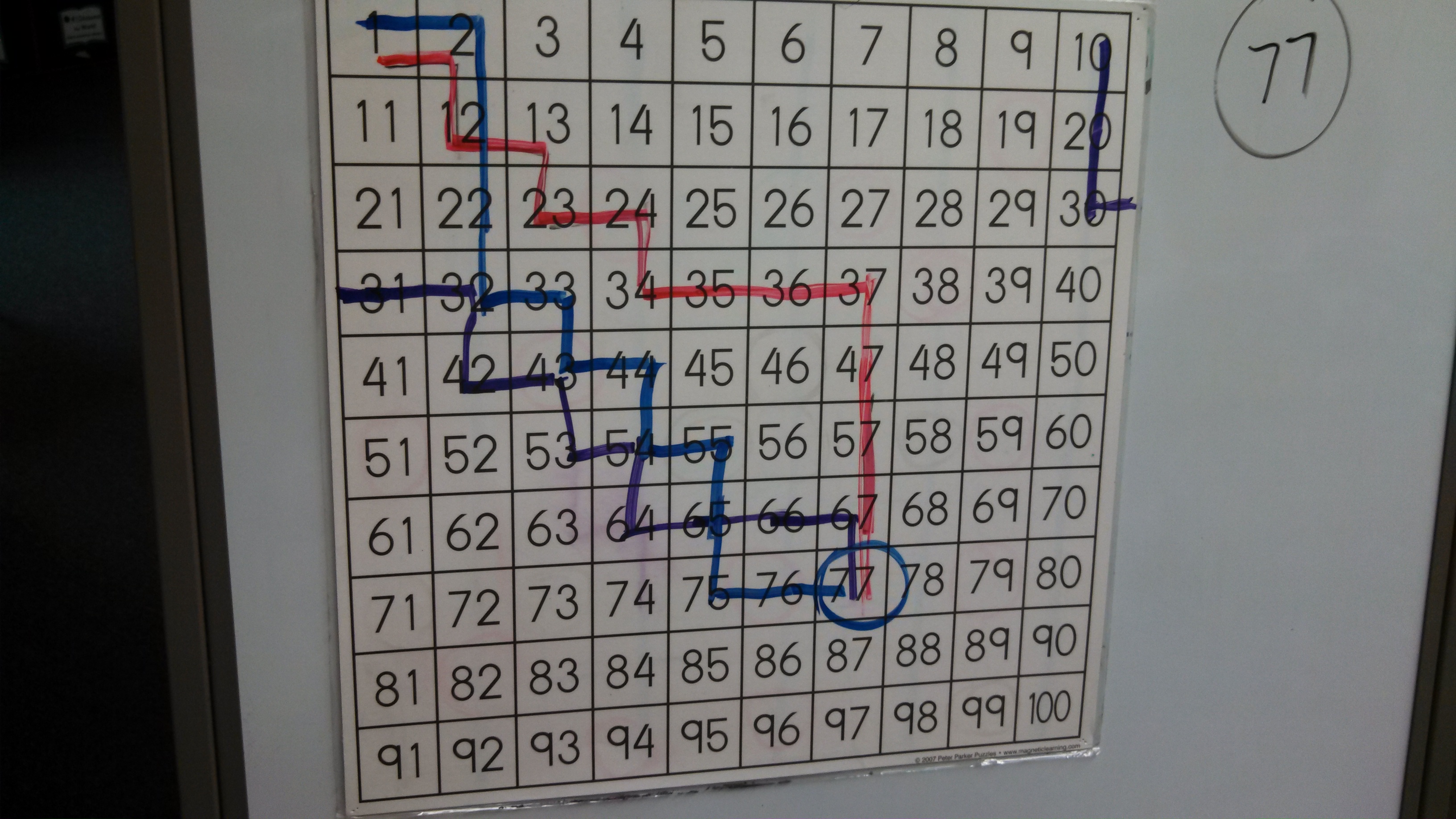
We tried clockwise and counterclockwise. We tried rearranging the kids by switching every third spot. For our last count, everyone stood up and traded cubes with somebody else.
What do you notice? What do you wonder?
Some of the kids’ claims:
“It will always be 77 unless we add some cubes or take some away.”
“It doesn’t matter what order we add in. It will always work out the same!”
There’s so much potential here.
Debbie’s planning to do the same thing with dimes and pennies on a different day. And, of course, we could give older kids multiples of ten and/or multiples of one.
After doing it just four times, we noticed an increasing smoothness for some of the kids. They were noticing that they’d either move over or down on the hundreds chart.
I’m excited to see what other versions we might come up with. Have an idea? Please put it in the comments!
And let me know if you’ve read about this idea somewhere else. Happy to cite it if we reinvented the wheel.
