I’m still coming down from the high of the awesome NCTM Regional conference in Nashville. So many good things were happening, especially in the coming together of NCTM and the MTBoS (Math Twitter Blog-o-Sphere). I’ve been thinking about my thinking and learning, and I find myself working over a few meta-observations. Here were the sessions I chose, plus the awesome #MTBoS mash-up keynote:
- “Motivating Our Students with Real-World Problem-Based Lessons.” Robert Kaplinsky, 6-8.
- “Get Your Model On: Mathematical Modeling in the Elementary Classroom.” Graham Fletcher and Mike Wiernicki. 3-5.
- I tried to go to “Model with Mathematics Using Problem-Solving Tasks” from Andrew Stadel, but I couldn’t get past the bouncer. 6-8. Instead, I hung out with Dane Ehlert, Michael Fenton, Michael Pershan, and Malke Rosenfeld.
- “Plan a Killer Lesson Today.” Kate Nowak. 9-12.
- “Using a Three-Lens Approach in Mathematics Professional Development.” Mike Flynn. 3-5.
- “Empowering Students with Rich Online Algebra Activities.” Christopher Danielson. 9-12.
- “Desmos and Modeling: A Mathematical Match Made in Heaven.” Michael Fenton. 9-12.
- And it killed me to miss “Fumbling toward Inquiry: Starting Strong in Problem-Based Learning” because of my flight. Super high on my wishlist. Geoff Krall. 9-12.
What do you notice and wonder? Here are mine:
I went with all twitter folks this time. Normally I have more of a mix, but I follow all these people closely online and there were several I’d never seen present in person. I had to address that.
Lotta guys. Hmm.
I checked out a lot of modeling, eh? Interesting. Unintentional.
I went to two desmos sessions because, as a mostly K-6 girl, I don’t play with it nearly as much as I’d like. I knew I’d have a ton to learn.
I picked eight sessions. Two of them were 3-5, which is my home base grade band. Two of them were 6-8. And four of them were 9-12.
What is up with that?
In the car back to the airport, Michael Fenton asked me what my conference highlights were, and the first thing that came to mind was playing with Christopher Danielson’s pentagons with Geoff Krall, Max Ray-Riek, Michael, and Christopher in the hotel bar Thursday night. I remember feeling incredibly happy exploring math with these people.
The other one that comes to mind, which I didn’t have time to tell Michael, was sitting in the back row of Christopher’s desmos session between John Mahlstedt and Julie Reulbach. Cathy Yenca and Mike Wiernicki were also there and lovely. I’d gotten to know both Cathy and Julie better the night before during amazing math education conversations over hot chicken, and it was great to connect with Mike in person as well. Christopher had us play Central Park, which I’d seen several times and played the first few screens of, but had never explored all the way through. Julie and John have used it lots, of course, but they were happy to be there and supportive as they watched me figure it out for myself. Julie played too, trying out new things and possible student solutions to see what would happen. And John was a great thinking partner for me as a newbie.
I’m not sharing these stories to drop names. I’m sharing these stories because there’s a common thread that interests me. I find myself hanging out with a lot of secondary people these days, and I’m happy to be there for a few reasons. Here’s why:
My Own Mathematical Learning
Over the past 15 years, since I first walked into Elham Kazemi’s math methods class, I have been re-learning elementary mathematics. My first time through, I was taught elementary math procedurally, like everyone else. It’s been a delight to figure out why the algorithms work, what the operations really mean, how ideas connect, and what strategies make sense in which situations. I still have tons to learn, which is why I am super bummed I missed Max Ray-Riek’s fraction division session. There’s way more ore to mine for me there.
That said, I have yet to re-learn most of the rest of my math, especially algebra. I learned a lot of formulas. Given the powerful experiences I’ve had re-learning elementary math, I know the delight of the a-ha moments ahead if I plunge into that stuff I memorized and figure out why it all works. I did learn calculus in an experimental, conceptual college class where we worked in groups and designed things and it was fantastic. It was also in 1991. I used a lot of calculus afterwards as a science major, but left that world in 1996. There’s 19 years of dust sitting on that thing.
So my first reason for attending all these 6-12 sessions is that I know I’ll learn and think about mathematics that I don’t get to learn and think about very often. I have long since stopped worrying about whether that kind of choice has practical application to my work in elementary schools. I know it does. The more math I learn, the better math teacher I am. I keep growing as a learner; I know more about where my kids are headed; and I understand more about what building is going on top of the foundation we construct in elementary school.
Solutions to Problems I Didn’t Know I Had
Dan Meyer was up in my neck of the woods a couple of weeks ago for the ATMNE conference, and I went to all three of his sessions. In Nashville, I went to Kate Nowak‘s session, where she posted this slide:

Dan and Kate both talk this way regularly. Motivating disaffected students to care about boring bits of math teachers have to cover is a pressing issue for them.
It’s not a pressing issue for me, in elementary school. It’s an issue, but not in my top five because we haven’t totally killed kids’ curiosity about mathematics yet. We’ve gotten better at covering less and spending our time on big ideas. The math we do actually does exist in students’ daily lives (kids have lots of experience joining, sharing, comparing, scaling, etc.). And, as elementary school teachers, we’re getting better at building off the mathematical ideas and questions students already have. All those things help with motivation.
So why do I go to talks about a problem I don’t have? Because the solutions to the problems are pedagogically powerful whether I’m facing apathetic teenagers or squirrelly first graders. For example, Dan’s done a lot of work (e.g., this series) around how we can create intellectual need so students actually have a problem they’re motivated to solve. (The ref on intellectual need is Harel 2013 and it’s awesome.)
Over the last couple of years, I’ve been mulling over how this idea of need applies in elementary school. Kids are more willing to do the work, but does that let me off the hook on need? I don’t think so. I have been toying with creating need – creating headaches, as Dan likes to say – in my teaching and it’s incredibly powerful. I’m thinking about conversations like this twitter thread, starting with these tweets:
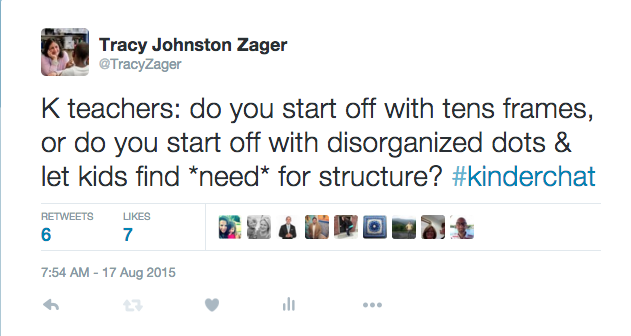
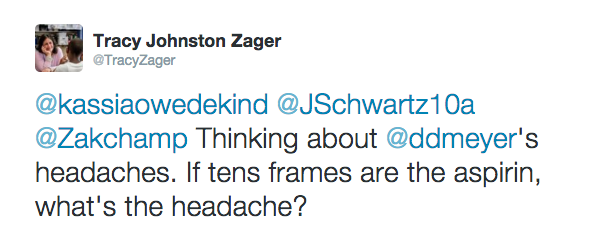
By the end of the conversation with all sorts of K-12 tweeps, we’d decided that, if tens frames were the aspirin, a disorganized heap of stuff made a great headache. We decided to introduce tens frames by making them available – alongside cups, bowls, and plates – during counting collections, hoping some kids would do what Joe Schwartz‘s kids did here:

Anyway, my point is that I wasn’t feeling this problem of the unmotivated student the way my high school colleagues were, but I am really feeling the power of their solutions to this problem. Their work is impacting my teaching in all kinds of good ways.
Here’s my wondering about that. What’s the corollary for my secondary friends? What pedagogical solutions do 6-12 teachers learn from K-5 colleagues about problems they didn’t know they had? I have lots of ideas about that, but I’m hoping you might share yours in the comments first.
The Question on My Mind
That wondering is all tied up with what I’m thinking about these days, from a professional point of view. This year, I began a new chapter in my working life by joining Stenhouse Publishers. As of January, I’ll be working half time as a Math Editor. I’m all kinds of excited and have lots of dreams about how I can use this position to give teachers platforms for sharing their ideas. I do a lot of thinking now about whose voices are missing from the professional development conversation, and whose voices are needed to impact education in positive ways that will help lots of kids and their teachers.
One of the great mysteries, to me, is what kind of professional development 6-12 teachers need. Elementary and secondary share so many instructional challenges, but others are so different and I have lots to learn. For example, I am so curious how teachers teach multiple sections. What’s it like to get to revise your lesson right away? I have to wait a year before I get to take another crack at most of my lessons. Julie Reulbach said, “Oh my God, you’re whole life is A period!” On the flip side, if I need 10 more minutes because of what’s happening in math, I can take it. I have flexibility, and I thrive on the variety of teaching 5 subjects. Another example: when I think about discourse with 30 kids I know really well, that’s totally different from discourse with 120 kids. Isn’t it? What happens with relationships with so many kids? And then there’s content. If I were to teach the same lesson 4-5 times this week, I expect I’d dig into that content and plan that lesson really deeply, in a way elementary teachers juggling 5 subjects rarely get to do. But then would I become committed to performing a lesson repeatedly, and get less responsive to where the kids actually are?
You could say the main question on my mind is how is instructional decision-making the same K-5 and 6-12, and how is it different? It’s not a long boil to get from that question down to this one: What do we have to learn from each other?
If the #MTBoS is any indication, a lot. My favorite picture from NCTM Nashville is this one:

Among these four people (and two pairs of cutiepie twins), I’m pretty sure you have deep experience teaching math at every grade level. In my professional life, I’ve only seen that kind of vertical collaboration in two places: conferences and the #MTBoS. The combination of the two is out of this world.
So, while I totally love my elementary peeps and tweeps and treasure the time we have to talk about both the content and pedagogical challenges we share, I also really love stretching myself by going to 6-12 sessions and learning about other content and pedagogical challenges. I’ve always been happiest on the steep part of the learning curve. Don’t get me wrong. I have tons more to learn about teaching elementary math, but I get a lot of value out of stepping out of my comfort zone.
One last word. This all only works if we support each other. When I was playing around on desmos among a group of people who know the task and the math inside out, I felt perfectly comfortable because I knew they were getting a kick out of me being there and stretching myself. Mistakes and misperceptions are part of the territory and everybody is down with that. In Michael Fenton’s session, there was a whole lot of math I haven’t touched in ages and is far from automatic for me right now. No sweat. That’s a fun prospect, and I look forward to taking the time to play with it when I can.
What’s the corollary? When middle and high school people want to learn about questioning strategies, academically productive talk, inquiry, the use of materials, small group work, listening to kids’ thinking, and looking at student work, elementary people are eager and willing to share. At least the ones I want to hang out with are.
Because, see, competitions over who knows more, who works harder, or who has a more challenging job don’t get us anywhere. What does? When we go to each other’s sessions, sit next to each other at the bar, do math together when we can, and interact with each other (not just follow) on twitter and in blog comments.
We each get to create the faculty lounge of our dreams here on the interwebs (h/t Christopher). Mine is populated with people who teach from kindergarten through college, who like to learn together and from each other, who make others feel welcome, and who listen with respect. That’s my dream.
It was awesome to connect in person with so many colleagues in Nashville. Thank you to the committee for all your hard work. I’m already pumped for Oakland/SF. See you there. You’ll find me in sessions both in and out of my comfort zone, meeting and talking with colleagues who span math education, picking up new ideas wherever I can.
Harel, Guershon. 2013. “Intellectual Need.” In K.R. Leatham (Ed.), Vital Directions for Mathematics Education Research (119–151). New York, NY: Springer.

