Yesterday, I was the lucky duck working with a team of three teachers who each teach multi-age 3rd/4th grade. We were all in one class together in the morning, and then got to meet during their common planning time later that day.
The kids have been working on perimeter, mostly of rectangles but also of other polygons. The first problem yesterday emphasized decomposing a 14-sided polygon into smaller rectangles in order to find the lengths of all the sides and then calculating the perimeter. Rectangles were in the air.
The second problem was this one from Investigations:
“The perimeter of Pilar’s yard is 100 feet. Draw a picture of what her yard might look like, and label each side.”
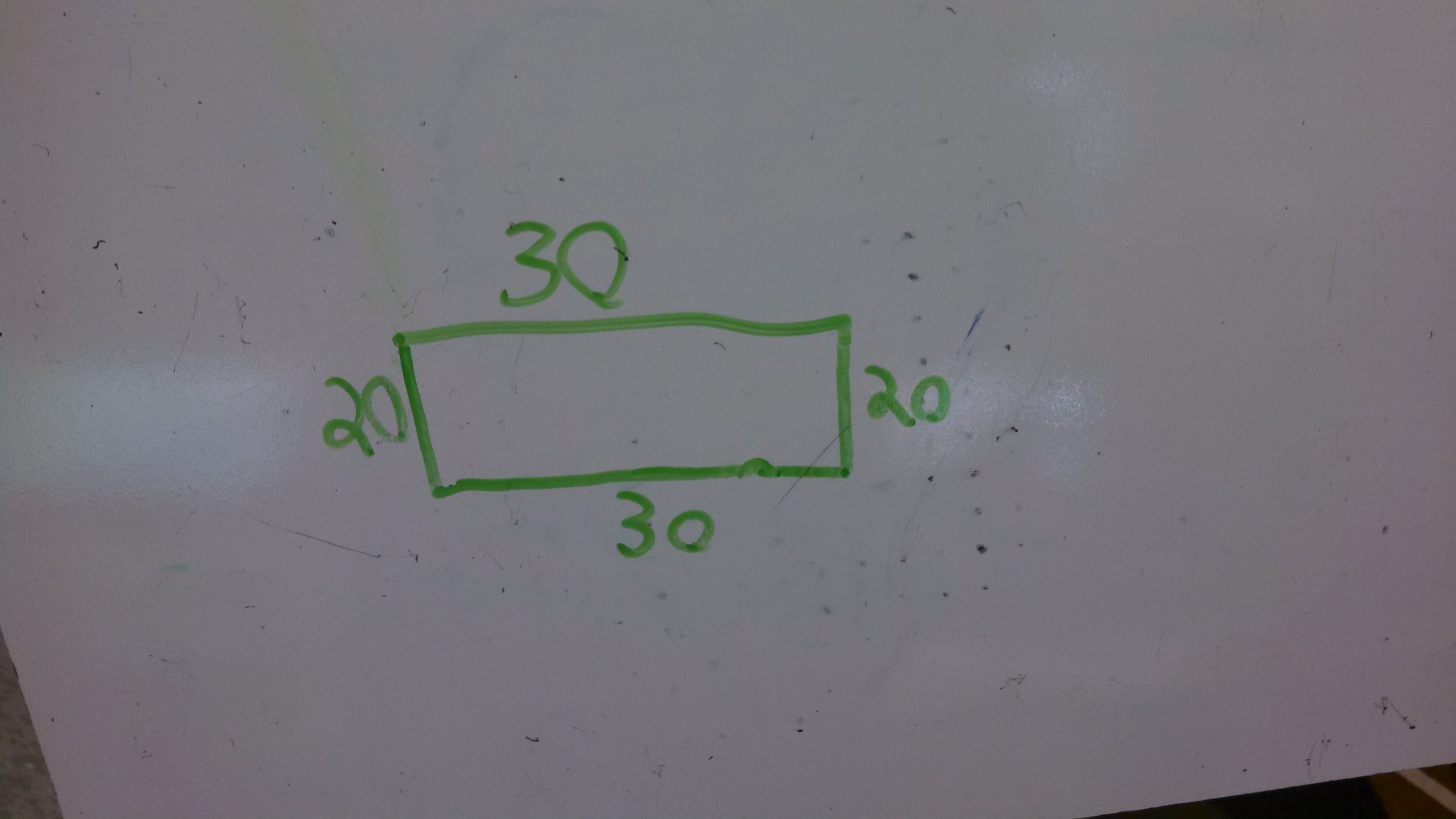
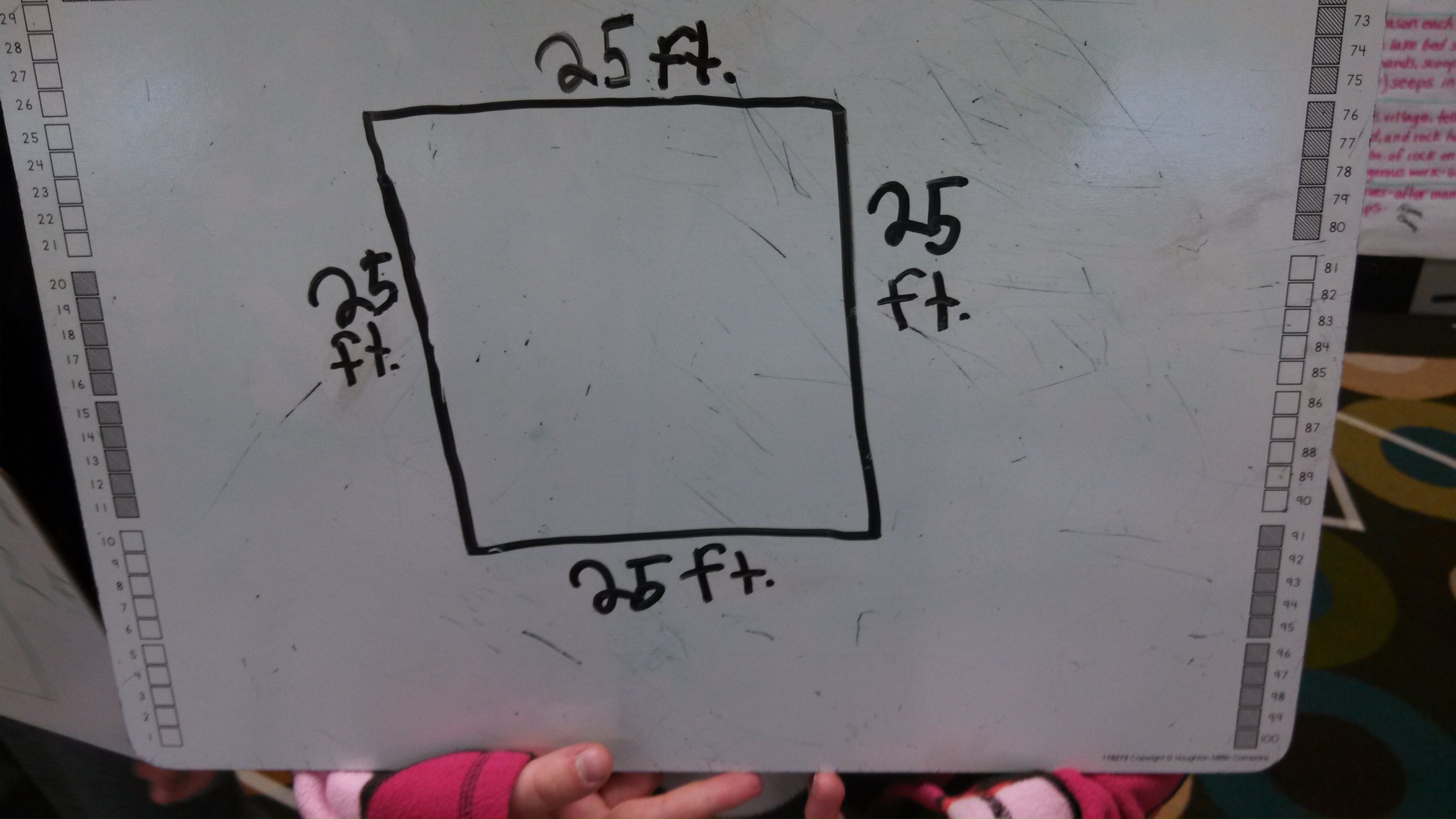
Unsurprisingly, we mostly got rectangles from kids, and mostly these two variations:
There was a little discussion at tables about whether this 25 x 25 square is actually a rectangle. Lots of kids have the classic misconceptions there. Oh how I wish we called squares “square rectangles” or “equilateral rectangles.” Sigh.
One student made a pentagon instead, which I totally loved.
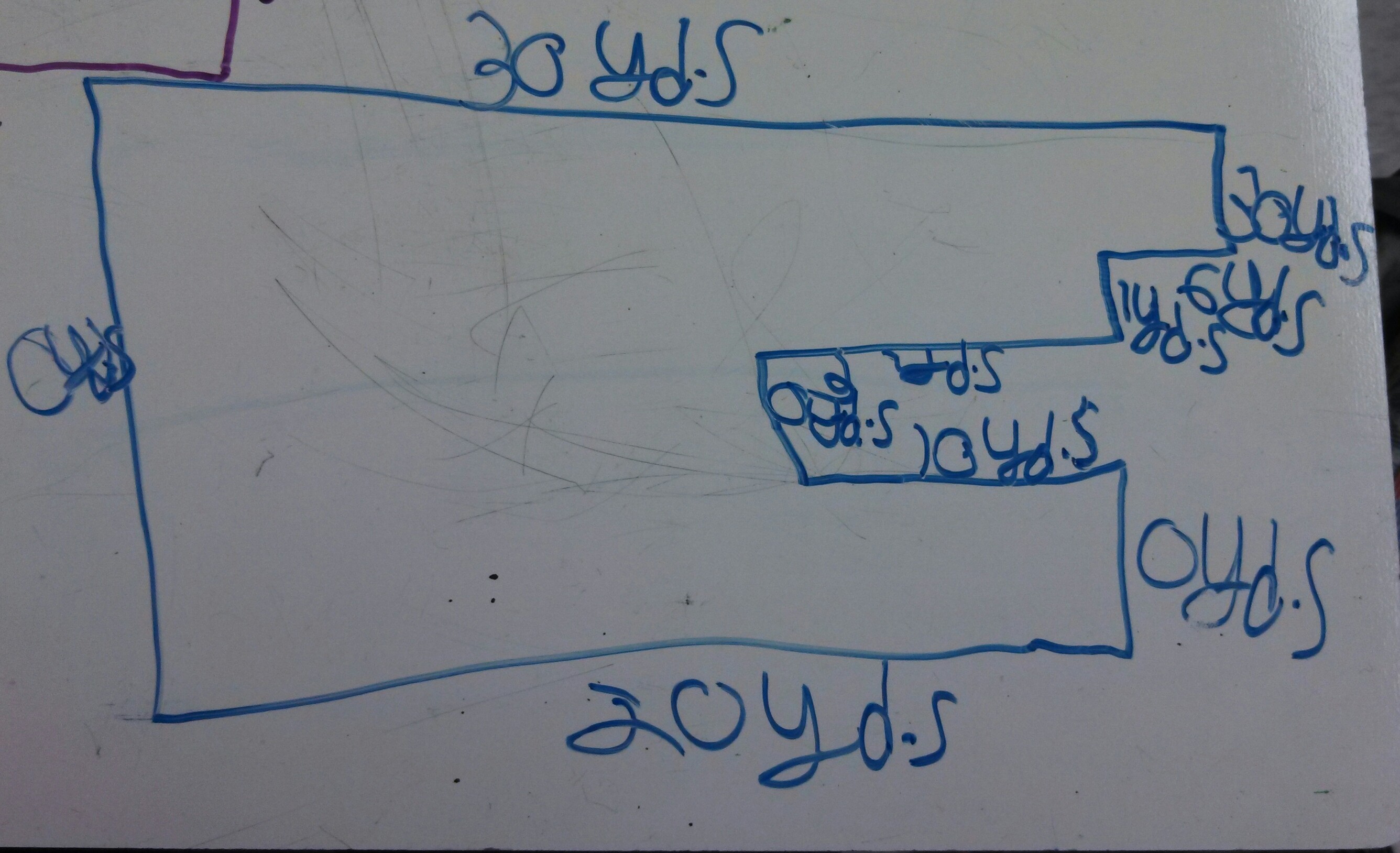
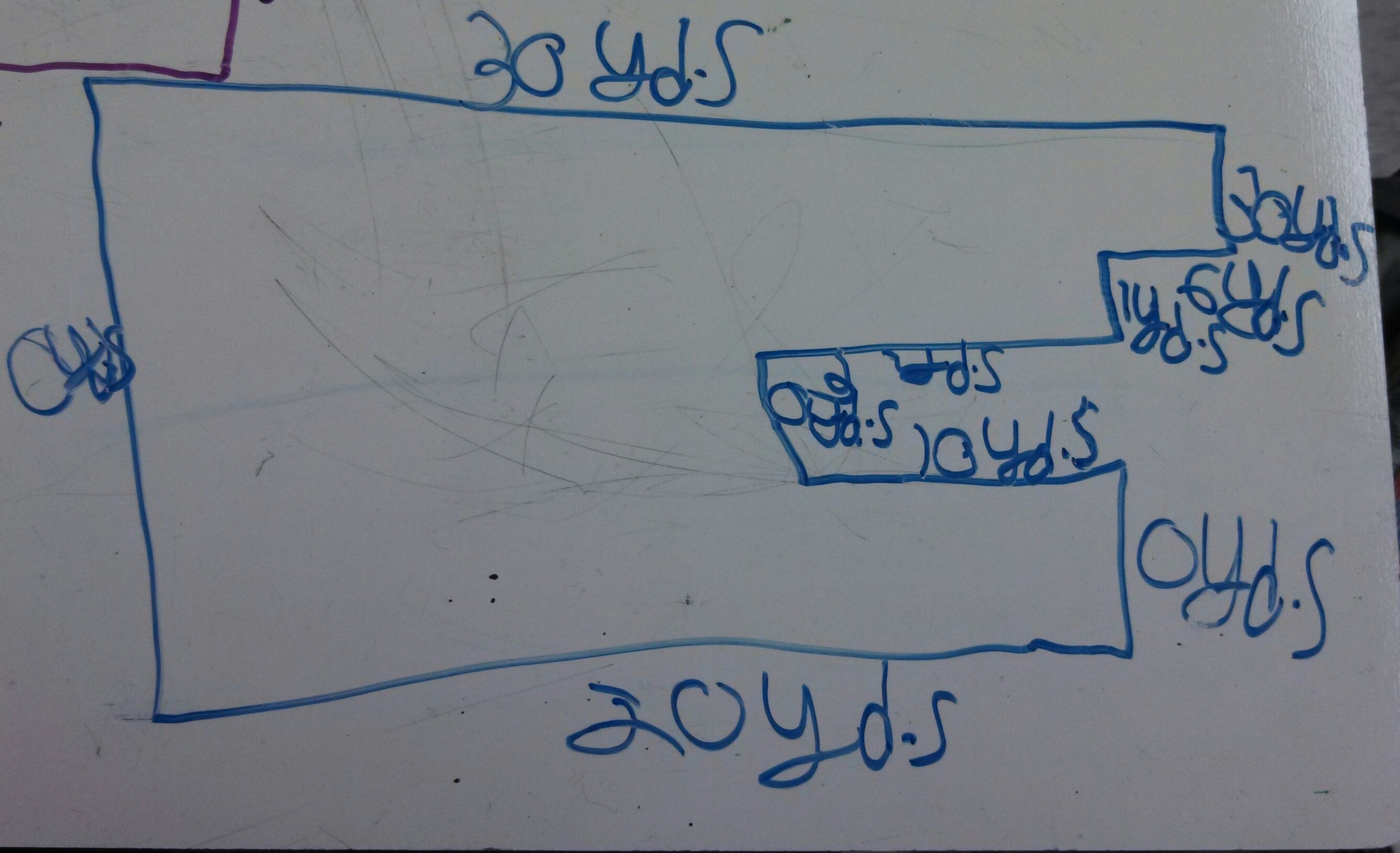
And then one student, pseudonym Jesse, made this shape:
Look closely. I noticed the dimension on the left-hand side is 0 yards. So are some of the ones on the right, but not all. I also noticed the long line across the top is 30 yards, and the series of short line segments on the right hand side that are all about the same length start with labels of 30 yards, 6 yards, 1 yard.
After the gallery walk, I headed over to Jesse. He made me laugh because he said, “I could see you squinting at my board from across the room!” I told him how cool it was that he took a risk and tried out a different shape, and I asked him how he did it.
“I made a cool shape, and then I started putting numbers down. But the problem is I used up my 100 and I still had a lot to go, so I made some of the lengths zero.”
“Interesting. I’m wondering what would happen if you tried to build this yard?”
Jesse said, “You couldn’t. It wouldn’t work. The zeros would mess you up.”
I asked, “Do you think you could make a yard this shape, that does have a perimeter of 100 yards, that you could actually build?”
Jesse said, “Yeah, but I’d need to erase all the numbers and start again. I’d try smaller numbers first so I wouldn’t run out of fence.”
We had to stop talking then, but I grabbed his board to discuss with the team later at common planning time. The kids had moved on to talking about the third problem they’d worked on, which was to draw three different rectangles that all had a perimeter of 20 units. The teacher had them post different rectangles on the whiteboard, and we saw all the whole number solutions: 1 x 9, 2 x 8, 3 x 7, 4 x 6, 5 x 5. The teacher asked a money question:
“Do we have all of them?”
Love that.
One student, pseudonym Zeke, said “No. There are lots more. Like, I could make one that’s 15, 2, 2, and 1. They add up to 20 also.” He held up a piece of paper that had a mass of zigging and zagging and curving lines and pointed to it as evidence.
This was the most interesting moment of the math class. Both the classroom teacher and the paraprofessional physically moved toward Zeke, lowered their voices and started talking at the same time:
“No, you can’t because…”
“Remember, you have to make a rectangle and rectangles have…”
In keeping with the norms we teachers have as a team of learners, I paused my colleagues for a second and asked if kids could discuss Zeke’s claim instead? Thumbs up. I asked the students whether they agreed or disagreed with Zeke’s statement that a rectangle could have side lengths of 15, 2, 2, and 1?
Students discussed the claim at their table groups. As we listened in, we heard a few useful arguments pop up. Some tables talked about both pairs of sides of rectangles needing to have equal length. Other tables talked about whether you could make a closed shape with those dimensions. Other tables were full of kids trying to draw a solution to his challenge.
We also noticed, though, that several students said you could make a rectangle with those dimensions. They had different, confusing arguments, and they weren’t leaning on the properties of rectangles at all.
And we noticed that no group had put together all the pieces. There might be one student talking about opposite sides having equal length, but they weren’t putting that property together with other properties of rectangles in a coherent way.
Time was up and we left it there.
At the end of the day, we were so glad to meet at common planning time. The classroom teacher thanked me for stopping her from correcting Zeke, and thought his claim made for a worthy discussion. We talked a bit about this—about how to view mistakes as opportunities in the classroom, and to free ourselves of the pressure to correct kids right away. We talked about not worrying that posting or sharing wrong answers will confuse kids. We talked about this lovely feature of mathematics, which is that we don’t have to jump in as the authority figures of what students “can” or “can’t” do; rather, we can trust that, in almost all cases, students can determine the truth for themselves by delving into the mathematics. This quote from Making Sense captures this idea beautifully:
“In traditional systems of instruction, teachers are asked to provide feedback on students’ responses, to tell them whether or not they are right…this is almost always unnecessary and usually inappropriate. Mathematics is a unique subject because…correctness is not a matter of opinion; it is build into the logic and structure of the subject…There is no need for the teacher to have the final word on correctness. The final word is provided by the logic of the subject and the students’ explanations and justifications that are built on this logic” (Hiebert et al. 1997, 40).
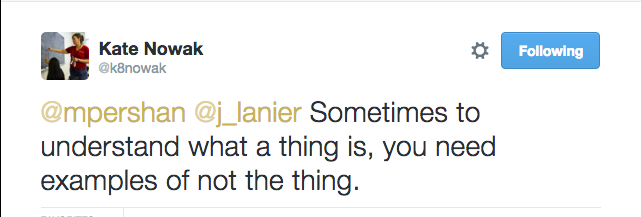
We also talked about the importance of non-examples, which made me think of this perfectly put tweet from Kate.
I told the teachers that, as a 4th grade teacher, I always had to teach kids what rectangles are. Kids pick up the crummy board-book definition of rectangles as shapes with 2 long sides and 2 short sides and square corners. (All the more reason why I can’t wait to publish Christopher Danielson’s better shapes book next year!) As teachers, we need to create conditions for kids to add depth and sophistication to their understanding about shapes. I thought Zeke’s claim was a fantastic opportunity for students to think about what a rectangle is and isn’t by focusing on the properties of rectangles, not just visual arguments.
The four of us kicked ideas around for where to go next. We had this open question: could you make a rectangle with side lengths of 15, 2, 2, 1? We all felt like the kids should take that question up by trying to build the rectangle. We settled on this plan for today:
The teacher would give each student 20 toothpicks and define each toothpick as one unit long. She’d ask students to make all the rectangles they could using all 20 toothpicks, without breaking toothpicks. They’d synthesize their list of rectangles to see if they had all the whole number solutions. Then they would take up Zeke’s challenge. Could they use their toothpicks to construct a rectangle with side lengths 15, 2, 2, 1? The teacher would use this exercise to draw out the definition of a rectangle, focusing on properties.
I wish I were going to be there today so I could see how it goes!
The four of us moved on in our planning time, and I showed them Jesse’s diagram for the 100-foot perimeter problem. This one.
Nobody had noticed it during the lesson, and we had a great conversation about it. And then the classroom teacher laid a whopper of a question on me:
“Do you think I should take up this work with the class?”
Holy smokes. So much ran through my head right then. Mostly, I was thrilled, overjoyed, elated by her question. Remember, earlier that day she had started to correct Zeke instead of consider his claim. I had just spent all this time trying to help this group understand the value of a piece of student work that reveals mathematical misunderstandings, or provides an opening to dig into a rich piece of mathematics. She was obviously listening and learning!
Once we decide to teach this way, though, the questions get harder, not easier. If we’re going to be responsive to what our students do and say in mathematics, how do we decide what to respond to? What makes for a worthy mistake to take up as a whole class? How do you know? By what criteria? We obviously can’t launch deep investigations into every single piece of student work, so how do we decide which ones to pursue?
This is one of my favorite things to think about. There’s a penciled-in plan for me to write a second book after I finish Becoming the Math Teacher You Wish You’d Had. The working title in my mind has always been Teaching from Mistake to Mistake. I want to get into these thorny questions of how we respond to students’ mistakes, what mathematics lies underneath different mistakes, what mathematical goals we have for our kids, how we decide which mistakes to take up in a big way, and how we decide which mistakes not to take up with the whole class. These kinds of instructional decisions are the ones that keep me learning and growing as a teacher. They’re also the kinds of complex instructional decisions politicians with simple answers and writers of scripted curriculum DO. NOT. GET.
So, as a group, we talked about what mathematical issues would emerge if we took up Zeke’s claim or if we took up Jesse’s work. My counsel ended up being that more students would benefit from the exploration of Zeke’s claim because the kids really need to investigate the properties and attributes of a rectangle. In my conversation with Jesse, it became clear to me that he wanted to head to a place of guessing and checking different perimeter lengths to see if he could sum to 100. There’s lots of fun math in that, but I think we’d end up investigating addition more than geometry, and the teacher’s goal is a deep investigation of geometry right now. I also think Zeke’s claim is accessible to every student in the class, and all students would benefit from exploring it. We talked about giving Jesse time to try to solve the problem he’d set out for himself because there’s powerful learning he can do. Of course, if his work spreads so other kids are trying to solve such complex problems during their next rainy-day recess, awesome. But Jesse’s diagram is not nearly as accessible to all kids, and I’m not convinced the time it would take for all students to make sense of it would have enough of a mathematical payoff to justify that use of class time.
It’s not a clear-cut call, though. I have mathematical reasons to say class time would be better spent testing Zeke’s claim rather than trying to make sense of Jesse’s work. But am I considering the right factors? Is it the same call you would make? How do we answer this question: which mistakes are worth pursuing as a whole class? I hope you’ll give me some pushback and ideas to think about in the comments.
*Update*
The teacher wrote me and told me how the toothpicks exploration went:
“The toothpicks worked great! I encouraged them to move them around and see if they could make Zeke’s suggested rectangle measurements work. It didn’t take them long to realize there was no way to make it work and most kids said for one reason or another. Yet I pushed them further to list ALL the reasons that it could not be a rectangle, based on what they have previously learned about rectangles. It was a really good math discussion to not only clarify all the characteristics that make a shape a rectangle, but to demonstrate how you need to prove it with facts – plural! That the argument one way or another gets stronger with more facts.”
References:
Hiebert, James, Thomas P. Carpenter, Elizabeth Fennema, Karen C. Fuson, Diana Wearne, Hanlie Murray, Alwyn Oliver, and Piet Human. 1997. Making Sense: Teaching and Learning Mathematics with Understanding. Portsmouth, NH: Heinemann.