Between NCSM/NCTM, spring break in New York, and then a big surgery, I’ve been off this space for a while. The teachers with whom I collaborate–the amazing staff at Rollinsford Grade School in New Hampshire–have been going full steam ahead, though, and they’ve taught me so much more about young kids and number lines! I’ll do the best I can to recreate what went down after my last post, Building Number Lines in Kindergarten, where we played with number lines in Becky Wright’s class.
In both the exceptional comments on that blog and through our experience, I learned that the big ideas would take a lot more time. If I’d mistakenly thought we were done, though, Daphne was going to school me. She’s my 5-year-old daughter, and she had joined me in Rollinsford for the number lines day. The next morning, she approached her regular kindergarten teacher and asked if she could set up a station to teach number lines to her class, like she’d learned in New Hampshire. I can’t begin to describe how happy these pictures made me, both about Daphne and about her kindergarten teacher’s openness.
At home, Daphne asked to make more number lines. I put tape up the stairs to see what she would do. Perhaps the rhythm of the stairs would come into play? Nope. She measured by marker lengths instead.
Then she decided she wanted to fit 100 numbers, so she started squishing:
Back in Rollinsford, Deb Nichols had loved the lesson, and decided to try it out with her 1st and 2nd multiage class. She put tape lines down for students to work on, and found her kids did just what the kindergarteners had done: they created number lines where all the numbers were squeezed together. When she asked the kids to spread the numbers out, the students weren’t any more concerned about equal intervals than the kindergarteners had been. Deb decided to put together a slideshow of things that come in regular intervals to see what the kids would notice. (We’ve been gathering more pictures at #intervalchat over on the twitters):
As students were noticing and talking, they developed a need for a word to describe these spaces, so Deb introduced “interval.” The kids headed off to lunch, and we met as a team to brainstorm. We were curious if exposure to all these intervals would infiltrate their thinking about number lines. After lunch, we all went in to co-teach, and Deb asked the essential question, “How do we know how to make the spaces on a number line?” Kids had some suggestions, like using rulers, or sticks if we were in the woods. One student talked about turning his line into a measuring tape. This student turns out to know quite a bit about measuring tapes because he lives on a farm, and they frequently use “cow weight tapes,” which are my new favorite measuring tool.
By measuring the length around the barrel of the cow, the farmer can get a good measurement of the cow’s weight. Beyond awesome.
Anyway, we asked the kids if the intervals had to be even, and the students were mixed. We decided to leave that question in the air, let them at their number lines and see what happened. Before they went, we reminded them that they could use tools around the room or their bodies to decide where the numbers should go. To open the possibilities a bit, we asked students how they might use their bodies. Several students stood up and demonstrated ideas like tip-toeing, crawling, jumping, or using their feet or forearms to measure. And then they got to work.
Interestingly, all the groups started working on evenly spaced intervals. I wonder if the rhythmic movement of their bodies on the number line got them thinking that way? At any rate, Deb had made the number lines around 8 feet long and asked for 11 numbers, so nothing obvious worked. Every pair got partway down their line and realized they would either run out of room or not have enough room to finish. And here’s where things got really interesting. In most groups, students went back to the beginning and tried again, with a different sized interval. For example, this group realized putting one cube between numbers wasn’t enough.
 They tried over and over, adding cubes to increase the interval lengths each time.
They tried over and over, adding cubes to increase the interval lengths each time.
This group was using a ruler (to create a descending number line–interesting).
They realized a full ruler was too much, and decided to switch to parts of rulers. They worked for an incredibly long time, trying different intervals. 9 was too much. 7 was too small. 8 was too much. They fine tuned their intervals into fractions of inches, which worked out great.
This pair tried using magic markers.
One marker was too small, so they tried to measure using lengths of 1 1/2 markers. Really challenging, especially on a wall.
Some groups changed strategies partway through. This pair used rulers. When whole ruler lengths didn’t work, they switched to their own feet.
To my eyes, these groups were all trying a similar trial-and-error approach, with varying degrees of success but exceptional perseverance, communication, and thinking. Great stuff. Two pairs did something very different, though. When they realized the original interval length they picked wasn’t going to work out perfectly, they didn’t go back to the beginning and try a new length. Instead, they changed intervals partway down the line.
This pair started with one student’s feet, without sneakers. At about this point, they realized they were going to have too much tape sticking out on the end. So, they got thinking.
They measured, and realized the other boy had longer feet. He took over for a few intervals. As they got to the end, they realized they still were coming up short. Their last interval was the two students’ feet, added together.
Kids are brilliant.
In another pair, they got about 2/3 of the way up the wall using 12″ rulers when they got to their “uh-oh” moment.
 I asked what was happening, and this student explained that the tape would have to go all the way to the ceiling, or higher, for him to fit all the numbers. The teachers and I thought he really understood the problem, and was going to go back and create smaller intervals. Instead, he switched to using a bolt instead of a ruler, and finished his number line with a series of smaller, equal intervals.
I asked what was happening, and this student explained that the tape would have to go all the way to the ceiling, or higher, for him to fit all the numbers. The teachers and I thought he really understood the problem, and was going to go back and create smaller intervals. Instead, he switched to using a bolt instead of a ruler, and finished his number line with a series of smaller, equal intervals.
Wow. Ever since this lesson, I’ve been noticing how often I see interval lengths adjusted like this. For example, check out the rivets on these posts in a New York City subway station. Look at all similar to his number line?
I have come to notice that we change interval lengths all the time in construction, when spacing telephone poles, when putting stripes on shirts. But, these examples are not number lines. There’s an important difference. On a number line, lengths are arbitrary, but they mean something. Ha! How’s that for a philosophical statement? But, I mean it.
When we make a graph or a number line, we set the scale. We decide what the unit is. How big is 1? Or, how big is 1,000, or 0.2, or 1/8? We get to decide our scale, but then we need to stay consistent with it. If the distance between 1 and 2 is 1/4 inch, then the distance between 17 and 18 is 1/4 inch, because a length of one is a length of one, wherever it occurs on the number line. I learned from reading Andrea Petitto’s “Development of Numberline and Measurement Concepts” that Piaget termed this idea the “equal interval principle,” and it’s key to children’s developing understanding of measurement. As far as the number line goes, kids need to learn the equal interval principle and conservation of length in order to move beyond thinking about position and sequence on the number line, and start to think in terms of proportion, distance, and space.
Also, I’m always excited when we have an opportunity to introduce the idea of authorship in mathematics. So often, math is presented as if it’s separate from us, and immutable, and impersonal. This little primary number line lesson, though, shows that each of us has choices to make when doing math. Whoever authors that number line decides what one is. That’s a pretty big thing to decide.
So, all this was rattling around in my head for a bit, and then my daughter Maya’s teacher asked me to come teach a lesson in 2nd grade. Last year, I helped her out once a week in math, but had to stop when I was diagnosed with cancer this September. This would be my first time in the math class all year. Maya had told her about the number lines, and she wanted to try it out. I knew from homework that Maya’s class was working on money. I thought it might be a kick to see what happened if we put money on the number line.
I started out asking the kids about the number line. They’re given number lines on worksheets all the time, but they’ve never made their own. After some chatting, I asked the kids what questions they had about the number line. Two standouts:
What do those little lines mean?
If we don’t write the numbers on the number line, are they still there?
Holy crow do I love that last question. These kids have been adding and subtracting on the number line for a while, so they can kind of use the number line, but they clearly want to think about the number line. I was psyched.
I put tape lines down and told them they were “one dollar long.” (I had made the lines long enough that kids could have put 100 pennies down. That’s important.) I asked pairs to choose a denomination (pennies, nickels, dimes, or quarters), and then grab a bag of play money and place the coins where they belong on the number line.
This was hard stuff, especially for kids who did not yet have the equal interval principle:
But, after some monkeying around, all the pairs placed their first set of coins, and then taped where the coins had been. Now, this was my favorite part. We asked them to choose a second set of coins to place. All kinds of good stuff happened.
Some groups completely ignored their first set and placed the second set without concern. But then, they started to think about the numbers related to each other. Where should 25 go in relation to 20 and 30? Before long, kids were using one set of numbers to orient themselves on the line and place the other set.
Seriously, how beautiful is that? I heard kids really connecting money and number lines and skip counting by 5s, 10s, and 25s:
“If you count by nickels first, then you’ve already got all the numbers there for dimes and quarters.”
“In between every set of dimes is a nickel.”
“Quarters always land on nickels, but only sometimes land on dimes. That’s because of the 5.”
I didn’t expect Maya’s teacher to have much time to continue to play with the lines, but she left them down and said she’d try to find time. The next time I stopped by, she told me the kids all wanted to add the other coins, and had:
Looks to me like they developed the need for those little lines after all. They even developed ways to demarcate different units with different tickmarks, eh?
I wish I’d been back in the class. Of course, I would have revisited their questions:
What do those little lines mean?
If we don’t write the numbers on the number line, are they still there?
And I think I would have asked them whether the intervals need to be equal, and why. I wonder what they’d say?
—
Updated here: https://tjzager.wordpress.com/2015/05/18/number-lines-addendum/
—
FYI, @bookgirlkpr shared this lesson study around number lines and kindergarten on twitter:
@MatthewOldridge @TracyZager @drcathybruce Here is an interesting lesson study for number lines in kindergarten. http://t.co/l2WWsSMNSX
— Sandy (@bookgirlkpr) May 5, 2015
http://www.tmerc.ca/m4yc/peterborough.html
Petitto, Andrea L. 1990. “Development of Numberline and Measurement Concepts” Cognition and Instruction. 7(1):55-78.























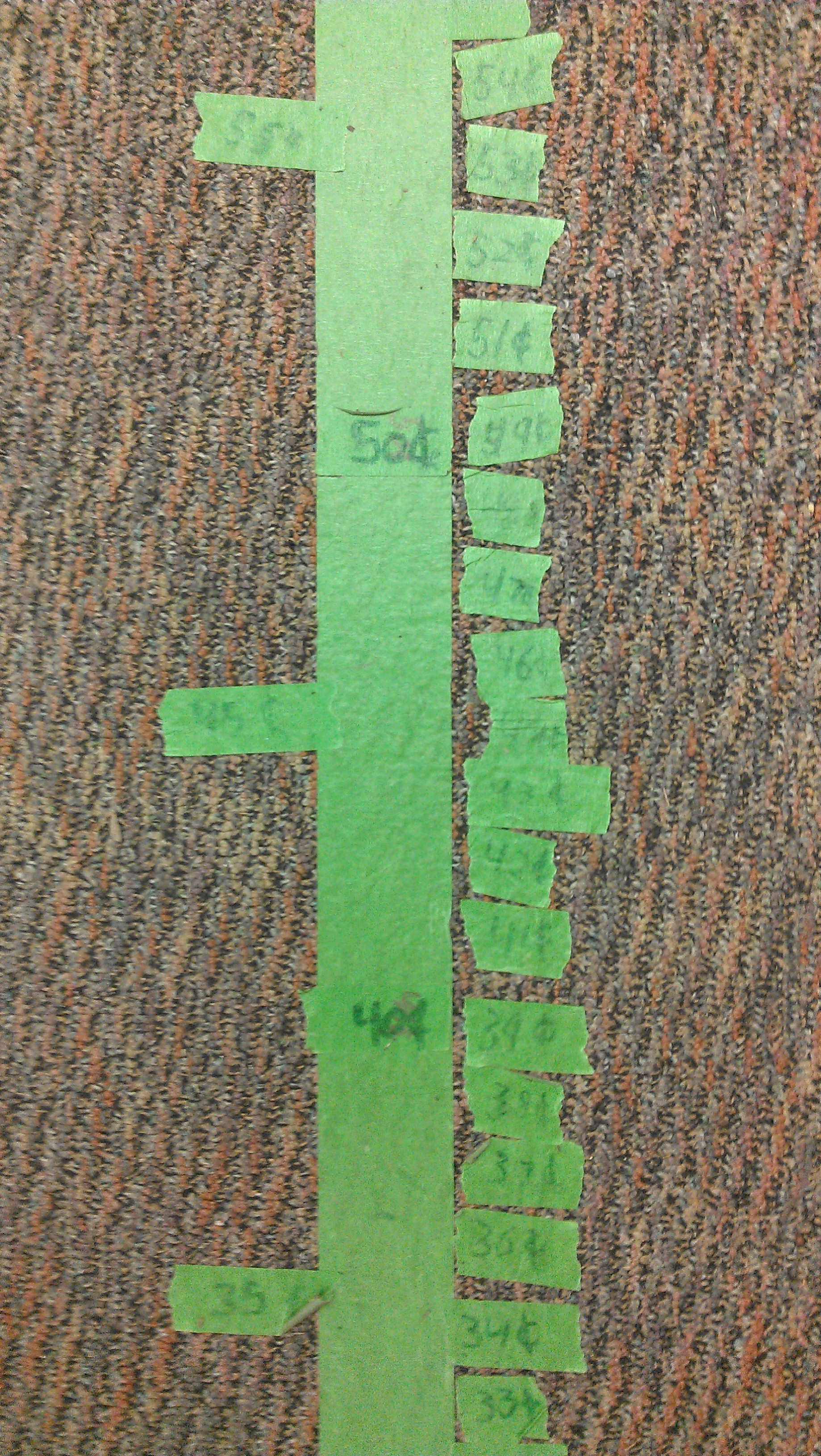

Holy crow, that was an inspiring post. I’m amazed they could think of a line as a dollar long. I would have thought that would be really hard. and now I’m going to be obsessed to see if I see intervals that change in the middle. So of course I’m thinking about how to relate this work to building number lines with fractions in the upper grades because fractions don’t even seem like numbers sometimes to kids or they see fractions as two different numbers. Question — it seemed like it was a good thing to have the number lines not premeasured to “work” with any particular interval, right? I’m interested in all the different kinds of things students were using to measure. And I think it makes a lot of sense that Daphne wanted to fit 100 into hers and that made her not be as concerned about intervals. So much good stuff here Tracy. You must be feeling good to have sat down and written all this.
Holy crow you’re speedy! I was also glad they could think of a line as a dollar long, and that they didn’t get hung up in the difference between the length of the jumps and the number on the line (jumping by dimes…10, 10, 10; writing on the tape 10, 20, 30). I think both of those ideas are hard!
There are tons of possibilities with fractions. I actually think money leads into that idea so well, and I never would have made this connection before. But, with money, they KNOW there are numbers between the other numbers. They believe it. So we can establish this idea of numbers between other numbers we can see on the line using a familiar context.
And yes, it’s important they don’t work with a pre-measured interval. But I did measure the play money, and pennies were 3/4″, so I made sure the tapes were at least 75″ long. I think they were in the 80s. I’m so glad I did. I love that the kids put all the pennies in between.
In Deb’s room, the mix of nonstandard and standard measuring units was fantastic.
(I’m starting to feel like myself. Twitter first, then blog, then NCSM proposal, then I will be ready to write my book again! Miss you! xo)
The skip counting with coins is spectacular-
“Quarters always land on nickels, but only sometimes land on dimes. That’s because of the 5.”
Great!
I love the foundation for factors and multiples here. One student pointed out that all the different coins landed on 50 cents, but only pennies landed on some numbers, like 11. Well isn’t that interesting?
I wonder what happens if you introduce a new coin, say, 3 cents. (Maybe of the students’ own design.) If you put the first one at 3, then I expect they could place coins up till 99.
But would they notice anything about 3 cent coins and nickels, and when/where they overlap?
Only one way to find out… 🙂
Awesome post Tracy! I completely was thinking fractions the entire way through. It would really draw out the meaning of the denominator when students created intervals based on different objects on equal length (1) tapes. For example, if I used a penny, I could be breaking up the tape into 10ths but if using a marker, thirds. So, the smaller the interval the more intervals within one while the opposite is true with larger intervals. Are there objects that create different but equivalent intervals? How fun to see them investigate?
Always something new to think about!
Yes! That reminds me of Leandra’s post from earlier this year: http://themindfulmathematician.blogspot.com/2015/01/oh-its-number-line.html So good!
This task is so rich; it immediately had me thinking how does this relate to my 7th graders (fractions, decimals, percents, graphing) and how I can make learning more active for my students. Thank you!
You’re welcome! I hope you’ll keep me posted if you decide to try it out with the older kids. I agree, there are lots of possibilities!
If you’re looking for an easy way to teach kids how positive & negative numbers work this board game gives a great visual demonstration:
Kids go up & down the board in steps, learning how negative numbers work.
Creature Quest
https://amazingwizkids.com/product/creature-quest/
It’s very simple to play & gives a great visual to help kids get the concept that the number line runs both ways and to help the concept become less scary.
Thanks!