I’m so stinking lucky. I’m working with an amazing staff at a lovely school over weeks, months, and years, and I learn so much every day we have together. Yesterday, I spent my afternoon with the K-2 teachers, and we continued our ongoing discussion about number lines.
The kindergarten teacher at this school thinks so powerfully about how her kids think! The week prior, she’d told the rest of us that she’s been modeling using number lines as representations and tools, but she wasn’t sure how to help kindergarteners really own the number line. I loved that thought.
I turned to some of my favorite sources to see what I could find about introducing number lines. Kassia Omohundro Wedekind, thinker, writer, and kindergarten teacher extraordinaire, helped me tremendously. She emphasized the importance of teacher modeling, a la, “This is one way you could show what you just did on a number line.” She suggested using lots of board games where kids move game pieces and count jumps. She brought up developmental issues around drawing the number line with paper and pencil, and how it would be hard to tell if kindergarteners were struggling because of the math or fine motor skills. She talked about building a giant number line.
The teachers and I had also thought about constructing a big number line, so I also wrote Malke Rosenfeld, who is always thinking creatively about the intersection of math, dance, and painters’ tape! She was generous with her time and gave me a lot to think about. My biggest takeaway from our conversation was to avoid turning a giant number line into a giant worksheet. I can see how easily we could have moved right to having the kids “acting out” what we did with markers and pencils on paper. That would have been unfortunate. As Malke wrote me, “Working at moving-scale is really about opening up possibility for new insights about math ideas that is not accessible at hand-scale or in symbolic form.” Hmm. That’s interesting.
I also turned to my bookshelf, and spent a fair amount of time looking for good thinking about introducing the number line as a model. If anyone has good references, I’m all ears. I found most books just jump into using the number line, without thinking about how students would make sense of it. I did find a really interesting chapter in Cathy Fosnot and Maarten Dolk’s Young Mathematicians at Work: Constructing Number Sense, Addition, and Subtraction called “Developing Mathematical Models.” They focused on contexts for learning the number line, and included examples using bus stops and city blocks. Those examples were both from schools in New York City, where students have a tremendous amount of experience with buses, city blocks, and subways—all rich contexts for discussing the number line. The school where I’m working is in a small town in rural New Hampshire. The kids don’t ride buses or subways, and the numbered streets in the town center start at 2nd street and end at 4th street. These contexts weren’t going to work at all!
None of us could think of a familiar context for number lines in these students’ home lives. (If anyone has ideas for contexts, I am all ears. Please leave them in the comments.) I still felt like it was important to connect to something the kids were already doing or thinking about, so I went into the kindergarten room to look for opportunities. That’s when I saw this chart:
The teacher told me they keep track of how many days they’ve been in school using this chart. Just that morning, she’d added the second piece because it was day 121, and there’d been a lot of conversation about it. They also use the chart to look for patterns in number, practice skip counting, etc.
When we met as a team, we talked about using this chart as context. We thought about asking students what would happen if we stretched the numbers out so they were all in a line?
A quick thought about “real world” here. This chart is very different from bus stops and city blocks in that it’s already an abstract representation of numbers, rather than experience from students’ daily lives. What mattered to me wasn’t the “real-worldness” or not of the context, though. What I wanted to do was give students a chance to connect one idea to another; to make a bridge from something they knew to something new. Seeing math in the world around us is one huge type of connection (to borrow literacy terminology, it’s a math-to-world connection). Making connections from one mathematical idea or representation to another is also a huge type of connection (math-to-math, right?). Some of the best math lessons I’ve ever taught have involved comparing two different representations. I was happy to start with the chart.
As a team, we made some decisions:
- We’d have the kids work in small groups on long number lines, and see what happened.
- We decided that each group should pick a starting number off the chart. It could be any number they liked, but they had to come to consensus on that number.
- We decided having several different sections of the number line would work better than trying to have the groups each take a segment of one long line, and then attach them together somehow. An added bonus was we want students to know they can zoom in on any section of the number line and use it. They can start and stop anywhere, rather than starting at zero or one. We wondered if this approach might help them with counting on?
- We’d ask students to put eleven numbers in order on their number line because we wanted them to be able to make ten jumps.
- We’d give students sticky notes to use to work out their ideas, and then tape when they were ready.
- We decided to line the tape up with the floor tiles and see if any students noticed their regularity, and used them to place their numbers.
We expected students would struggle working together. That’s OK. Teaching how to work together is part of teaching, and teaching math. We expected sequencing might be hard for kids, especially because the chart is organized vertically. Otherwise, we weren’t sure what to expect!
All groups started the same way:
- They chose their starting numbers first (1, 2, 6, 13, 14, 15, 121—this lesson was inherently differentiated in that regard).
- They wrote their numbers on sticky notes (sometimes after arguing, sometimes after taking turns).
- They sequenced their numbers correctly (some groups used the chart to figure out the sequence—awesome).
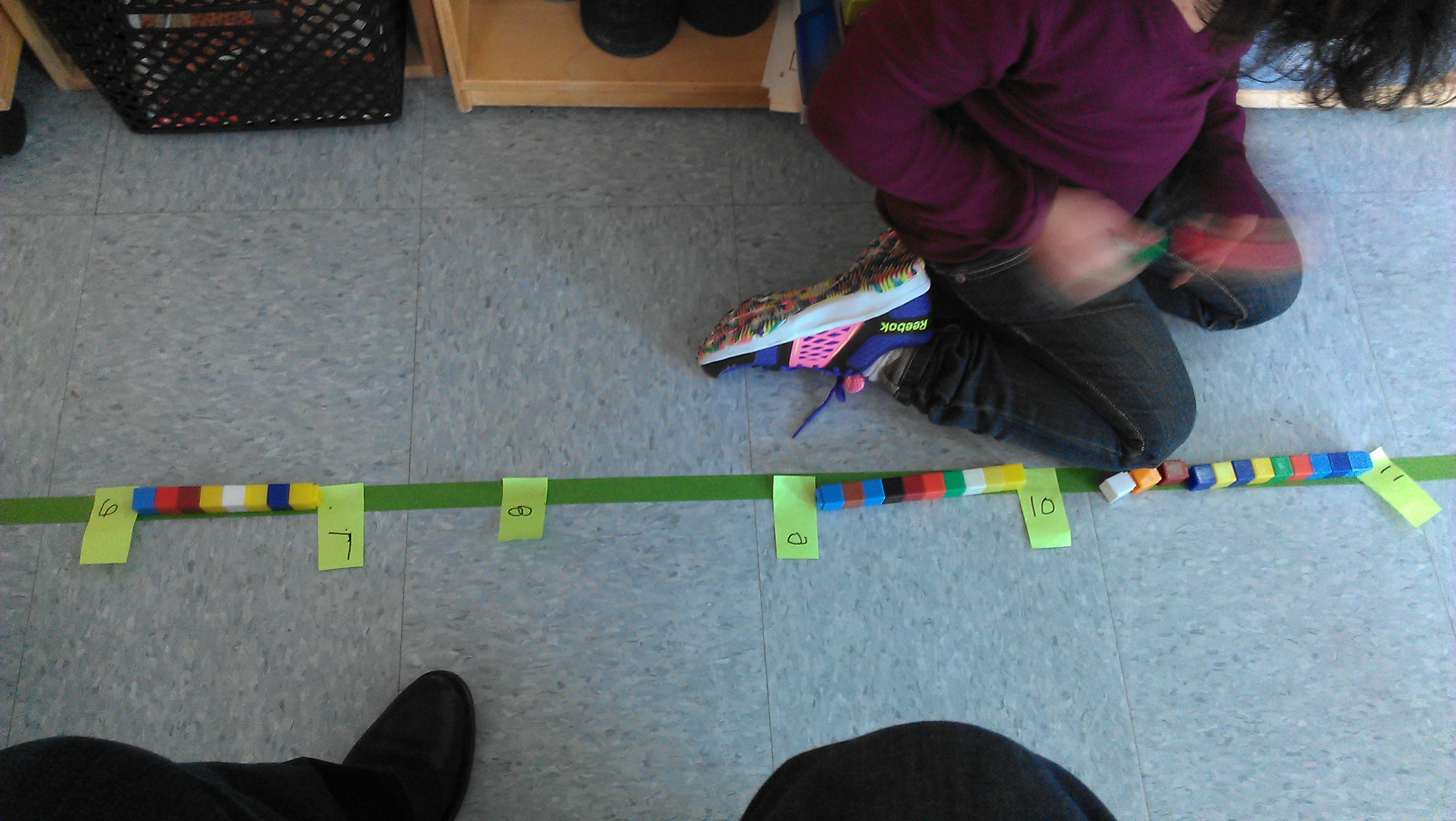
- They placed them side-by-side on their number lines, all scrunched up on one end:
Fascinating! We started asking kids, “Can you use more of the line?” That’s when the really interesting discussions started. One group immediately understood they could put more space in between their numbers. They started by inserting a “finger space” like they put between words. When they’d finished, they still had lots of line left. They tried again, this time inserting a “hand space” between sticky notes. Still too much room. At that point, they noticed the tiles, and decided to use them.
Their line was one tile longer than they needed, however, which brought up some interesting questions.
When we pointed out that the space between 15 and 16 was wider than the other spaces, the kids discussed what to do. They ended up asking if they could have a 17 so they could go all the way to the end but make them even. Great solution.
At this point, we decided to have the kids take a “walkaround.” We wanted them to learn from each other’s ideas. After kids had looked, we heard students say, “We could spread them out more!” Great! What we noticed, though, was most groups spaced out their numbers, but didn’t distribute them evenly.
Teachers ended up pointing out the uneven spaces to kids. Some of the kids were fine with the spaces being uneven, while others wanted to revise their thinking. In one group, a student used his sneakers to prove the spaces were uneven.
“See? On this one, my foot touches the two numbers. But on this other one, there’s some extra sticking out.” I was thrilled with this development. I hadn’t really thought through the measurement aspect of this lesson, but here it was. A groupmate of his took out some cubes, and snapped together a stick of them. I thought she would use her cube-stick as a consistent unit, and space all the numbers that distance apart. Instead, she created lengths to match each interval.
Not what I expected, but totally cool too.
We paused the kids here for just a minute, and had students share how they were using tools they found in the room—floor tiles, feet, cubes—to measure. We gave students another chance to work on their number lines. One group loved the feet idea, and successfully worked together to make an evenly spaced number line using their bodies.
I was so happy, because now there were at least two number lines with evenly distributed intervals of different lengths: the one marked off by tiles, and this one marked off by one student’s foot. What a great opportunity for kids to compare and connect! And, of course, I love me a good use of non-standard units.
Other groups taped their lines down with irregular intervals.
I’m realizing how powerful it is to use removable painters’ tape to make these lines. I wonder, as the kids explore with their lines in the coming days, if these groups will want to revise their thinking. The teacher works hard to create a culture where revising thinking is a big part of doing math, so it’s possible.
When we discussed the lesson afterward, we were happy with a lot of it. We had all watched the kids sliding up and down the tape, moving from one side to the other of the line, and jumping from number to number. Everyone was happy to keep the lines down on the floor for a while, and see what happens. We talked about different ideas to create more opportunities for the kids to play with body-scale number lines, and decided to add a permanent one all the way down the K-2 hallway. The principal is going to have some number lines and hash marks painted on the blacktop outside, and teachers and students will be able to use sidewalk chalk to write different numbers on them. They’re going to paint some board-game paths outside and get some giant dice. And they’re going to add numbers in each stairwell, going up and down (yay, negative numbers!) from the 0 level.
Students asked great questions during the lesson. For example, one student talked about their first number line, when the numbers were squished together. She asked, “If we kept the numbers that close together and just kept adding sticky notes, I wonder how high the numbers would go.” Me too!
Our one discomfort was we felt like we imposed the idea of regularly spaced intervals on the kids, without really developing a need. We had planned the lesson quickly, and were much more focused on ideas of sequencing and magnitude than we were on measurement. We didn’t anticipate that the spacing of the intervals would be the big issue. Now that we’ve seen what happened, we’re all left wondering how we could have the kids realize the numbers need to be evenly spaced? What would help them see a reason?
Ideas?
—
Update: Part 2 is posted.



















What a fun activity! Need to think about a natural reason for the even spacing. I once played a fun game on the number line with my kindergartner https://aofradkin.wordpress.com/2014/03/25/walk-the-line/
Thanks so much! I’ll take a peek.
Two quick thoughts about spacing the numbers evenly: one is, thinking of a body scale number line, one advantage to it can be the rhythm of moving on it, either individually (stepping, marching, skipping, etc.) or as a group. Having kids experience the rhythm of moving on their number lines while counting might lead to more thinking about the even spacing. Alternatively, next time you get to try this, you might have kids might experience the lines (with or without hashmarks) first without numbers on them, and then when their play inspires quantitative/measurement questions, the need for numbers to be evenly spaced might emerge. Questions about the lengths of different lines, how much farther kid A jumped than kid B, how far apart two friends are, etc. can be part of kids’ free play on the lines (and inspired by carefully set up teacher play ideas, a la the great Kassia!)
The second is, even spacing seems to matter most when the numbers have other numbers between them. In the world of sequencing and counting whole numbers, does it really matter if you say 123456 or 1…2……3…4……..5………6? I dunno. But what if you made card sets of your skip counting numbers (y’know, multiples, as they call ’em later on!) and looked at what happens when you have the 4s on there and you want to add in the 2s? It’s a bizarre context and maybe way too much for Ks, but it does get at how the numbers need to have gaps between them when there are other numbers in between them, and how the gaps should be evenly spaced to fit all the numbers that need to be there.
I love these thoughts, Max. The rhythm idea is fantastic. I totally love that! And I also love starting with a blank line and seeing what happens. Even asking, “How long is the line?” and seeing what kids do might get us there. If kids measure in different steps or strides or units, the idea of having uniform intervals may come up, while also showing that those intervals can be whatever length we choose.
I’m also thinking about the number line the (awesome!) principal is happy to put down the hallway. What if we made it a double number line, and counted by ones on one side and another number (probably twos) on the other? I’d love to have a conversation about where is the 3? 5? 7?
The 5/6 team is in a different wing of the school, and they talked about putting a fraction number line down over there. I’d love to take the younger kids on a walk over there and see what they think.
I was thinking about the spacing issue too. What about using the number line to count real objects? Posing a question to the kids about how to count and how to build a number line to show their counting. I’m picturing big, uniform objects, like pillows or book baskets…then the spacing would need to represent one object. You could then pose the question/model an unevenly spaced line (if they don’t come to it on their own) and ask if that shows the counting accurately. This also starts the transition to what the number line represents. Not sure how that would work… but was my initial thought! Great blog post!
Kate, thank you so much for your comment! We thought kids might pile cubes on the numbers: 1 cube on 1, 2 cubes on 2, etc. when they build their number lines as a way to make sense of magnitude. I was curious if this was likely to happen, and asked my 7-year-old daughter if she thinks about a number of objects when she thinks about a number on the number line. Her answer was, “No. I think of the number line as a river, and the numbers are the waves going by in a pattern.” Wow!
When I think about the big objects idea, I think we’d end up having a really interesting conversation because, well, is it one basket between 6 and 7, added to all the baskets that have come before, that makes 7? Is the idea that it’s the 7th basket from zero? Or are there 7 baskets on the number 7? I bet we’d see both. And how many baskets are there at -24?
This question of “what the number line represents” is a really complicated one! I’m sure there’s not just one answer. Last time I met with this group, some students had subtracted on the number line in first and second grades. Some kids used a take-away model, so if the problem was 51 – 16, they started at 51 and counted back 16 jumps to 35. Another student used a distance model. He started at 51 and looked at how far he had to go back to get to 16. He saw that space as 35. Same tool, different models.
The more I think about the number line, the more important it becomes to me that we preserve this flexibility. We can think about it in so many ways!
Again, thanks for your comment! It’s making me think. 🙂
Very useful post for me, as I got out our mini number lines this week. Next year I might start with this concept instead. This week I think I’ll get my painters tape out and back track a little. I will also check the Number Talks book for K-1 number line conversations.
Emily
Yay! I don’t think we have it quite cracked here, but it brought up so many interesting questions. Max’s comment above might be helpful. Keep me posted!
Tracy, after reading and reflecting on the process, I am going to give this a go this week with my 1/2’s. However, I would like to add some vertical number lines (doorways etc.) and some mid way on the walls. I will try to avoid the push for equal intervals and see what bubbles up in conversation. Have they yet really noticed all that they see and use daily? Can’t wait to send results to you!
Deb, I love these thoughts!!! You always take ideas to places I never dream of. I’m so lucky to work with you! Can’t wait to see what happens. Also, take a peek at the interchange between Max and me above. Might spark some additional thoughts you’ll run with!
Bouncing off Max’s comments, one thing to think about is that intervals are, by their nature, rhythmic. So adding in some kind of steady beat (regular intervals through time) along with movement (regular intervals moving through space) to the mix at some point might be really fun and useful to deepening experience with the idea.
Also, allowing children to get acquainted with the new line space during free time (maybe over the course of a few days**) allows you to really watch how they are exploring the space, what kinds of things they are doing with their bodies, what they are really noticing, and for *you* to develop some insight into their thinking that might not happen w/ hand-scale movement. After a few days of observing you could bring the class together to do a Notice/Wonder about the line(s) which would help you connect language to their body-thinking.
AND, at that point kids would have some experience on which you can create a different kind math-to-math connection. They may not have bus or subway stops, but you can recreate a similar experience with the line and tape at regular intervals. Spatial reasoning and exploration (especially spatial orientation — where you are and where you’re going, which is totally doable through tape on the floor) is a huge skill set for sense making in mathematics. And, although spatial orientation is a nascent skill in all of us at birth, it still needs to be developed through experience to be useful in learning.
**It might take a few days for you to see the full benefit of a line w/ regular taped intervals. Kids notice things in their environment and explore them with their bodies. I see this kind of thinking at the mall when kids walk the diagonals of a large tiled array of smaller squares. I see kids jump over cracks in the sidewalk. I see kids walk curbs one foot over another. All these are clues about how kids are thinking and what they are noticing about the structure of their environment.
Thanks so much, Malke. I think the idea of TIME is really important. In this case, I was only in the class for one session, one day, and we were hoping to uncover lots, which we did. But, I think you’re totally right, that if we remove any time pressure and just let the ideas develop, we’d be able to be more thoughtful about it and do more noticing. If you see Deb’s comment above, this is where she’s headed, just down the hall from the K. Should be so interesting!
I love the principal of this school, and she is really excited to paint some lines in and out of the building for kids to explore over time. So wonderful!
Real-world number line kids in NH may recognize their parents checking out: outdoor thermometer. Vertical number line with positive, negative numbers…
Wonderful day, wonderful post, Tracy.
Yes! Of course!
My thought, too… Outdoors in NH kids see he thermometer, and, let’s face it, this year they’ve seen negative numbers too!! Also, rulers. Yardsticks. Measuring themselves, their feet, etc.
Thanks, Susan!
Could the kids connect the number line in music class when they are reading music? They have learned 1/4 notes and how to “rest” – pausing for the same amount of time as the note itself. They have learned that 1/8th notes fit “in between” quarter notes, so there needs to be space in order for them to fit.
Maybe the older students could consider the 1/8th and 1/16th notes as fractions? I could picture the students maintaining a beat as they step on the numbers on the line, the faster the beat, the more numbers in between.
I’d also love to see us use the perimeter lines in the gym and modify them so to be used as number lines, too. “Line up” in PE could reinforce what is happening with number lines in math class.
Great idea, Julie! You might mention this to Kitri, Lindsay, and Noah, and the related arts teachers!
Wonderful post! Malke wrote about movement and rhythm with the number line, and I am in full agreement with that…let them feel the numbers in their movement. Hopscotch is a way that your students naturally do this. I also think that making artful number lines help to lend a feeling of importance to the number lines. I wrote about this in a post, which also talks about a way to scale the number line. https://bookzoompa.wordpress.com/2014/10/23/the-flux-capacity-of-an-artful-number-line/ In terms of relating their number line numbers to themselves, how about relating it directly to their own hands, maybe lining up handprints of the whole class? Here’s a post about doing this with children are learning to count to ten, which shows you in a miniature what I am thinking about https://bookzoompa.wordpress.com/2015/03/16/4225/
I would love to encourage you to somehow let the students know that this number line will stay with them throughout their math studies, and that it eventually becomes the x-axis when graphing. If the students can connect your vibrant number line activities with algebra, perhaps,then, when they see the number liner line as part of the coordinate plane, they will might feel like the are becoming reacquainted with an old friend.
Hi Paula,
Holy moly. I’m in love with this comment, and your blog, and your number line books! I must make some!!!
I will be writing these lines on a sticky note and putting them somewhere I see every day so I can think about it a ton:
“I thought that when I got to grown-up math that the lines would get longer. It never occurred to me that it would be the scale that changed, not the size of the line.”
This is a conception I’d never thought of explicitly, but I bet most kids are thinking this way! The student who asked how high we’d get if we kept the numbers closely spaced was on to this idea, I think. Seems worth a whole pad of sticky notes to pursue her question!
Also, I love thinking about more and better ways to connect the number line to the coordinate plane down the road. For most students, the coordinate plane feels like entirely new math, rather than an extension of what has come before. We can do so much better!
Thank you, thank you!
When I was thinking more about the length of a number line, I realized that even if we could make a number line that extended from here to the moon, it still wouldn’t be long enough! I was late in grasping the importance of scaling, so I am so pleased to be able to think about it so publicly now, and grateful that you’ve created this space for this conversation.
My 2 cents FWIW…
We’re asking students to order numbers and use an idea of “invisible” cardinality. We’re asking them to reason with something they can’t see, which makes open number lines abstract beyond belief (especially in kindergarten). There are lots of different ideas going on in this lesson but I see them more as part of a progression/trajectory, which takes a ton of time…starting here:
1. Can students accurately place a number on a partitioned number line 0-10?
2. Can students accurately place one number on an un-partitioned number line 0-10 and conceptually explain the position? (maybe by benchmarks of 5)
3. Can students correctly place two numbers on an un-partitioned number line 0-10?
4. Can students identify a position of “x” on an un-partitioned number line?
5. If they can, follow the same steps with 0-20, 0-50, 0-100.
The students appear to do really well ordering numbers beyond 20, which is amazing for kindergarten students. I agree with Max, in that I wouldn’t get hung up on the spacing of numbers. We’re asking students to estimate numbers and quantities that many still struggle to count. Identifying position of numbers on an open number line is more of a measurement skill introduced in 2nd grade (2.MD.6 https://commoncoretools.files.wordpress.com/2012/07/ccss_progression_gm_k5_2012_07_21.pdf pg.14).
Clements and Sarama also mention that integration and representational thinking of an open number line is employed mainly for the purpose of building computational fluency. Its in either Learning and Teaching Early Math or Learning Trajectories for Young Children. The reason I mention this is I don’t know if a “context” would necessarily help in this case, especially if students aren’t developmentally ready for it. I don’t think your forcing it either (knowing that was a concern). I’d look at it as “planting seeds” and leaving mathematical residue.
I’ve definitely donated more than 2 cents but there’s a great conversation happening here. Love what Malke suggests about letting them explore to see where they take it (which I know you agree with). Thanks everyone for making me smarter! And thanks Tracey for providing the forum to collaborate!
Totally interesting take, Graham! Thank you!
I would say–and I know you know this already–we had no intention of teaching anything to mastery here at all. The idea for the lesson came out of the recognition that we’re using number lines to represent computation (and cardinality) in K-2, but we’re not giving kids time to make sense of the line itself, without computing on it. So our intention was to give kids a chance to explore the representation; more of a “what is this thing?” than a “what can you do on this thing?” Thinking about it today, and in light of Max and Malke’s input, I’m thinking we did a lot, fast. Slowing down would really help!
That said, I think the kids were able to meet the number line wherever they were, and interact with it, and think about numbers and space and length in cool and different ways. As the teachers continue to give kids opportunities to play with it, I’m hoping the kids (and teachers!) will develop some new intuition about numbers, lines, and number lines!
There are so many thought-provoking comments here aren’t there!
I like what Graham’s saying lots, and also your point Tracy about getting a sense of numbers without rushing to do computation with them!
I love this! The number line is my favorite and I’m often thinking about ways to integrate it in younger classrooms. I love the connection to the hundreds chart, and could see this as a useful connection for teachers as well (I’ve talked to at least one 1st grade teacher who didn’t see the utility of a number line over the hundreds chart).
I worked with/on a team at UC Berkeley that developed a research-based curriculum for teaching integers (and fractions!) using the number line as the central representation: Learning Mathematics through Representations, aka LMR (available online for free at http://lmr.berkeley.edu/ My apologies for the re-direct, still working on that) (we’re also on facebook: https://www.facebook.com/LMRsite). An efficacy study conducted with 4th and 5th graders found that students (particularly students with lower initial understanding) made greater gains that students using the standard curriculum, and the curriculum has since been revised in line with teacher feedback and a focus on common core standards (see here for info on how it aligns with CCSS http://www.culturecognition.com/lmr/sites/default/files/CCSS-LMR%20alignment%20v1%20Oct2014.pdf).
I would recommend reading the full introduction to the curriculum before exploring any particular lesson, but I can’t help but point out this lesson in which students construct outdoor number lines in chalk (http://www.culturecognition.com/lmr/sites/default/files/PosInt4_Guide_Comp.pdf). The whole curriculum uses measurement (with formal and informal tools) to support creation and discussion of number lines (ack, I can’t stop linking to lessons, but I’m excited about the “finger pinch” and “pencil tip” images I made for this lesson: http://www.culturecognition.com/lmr/sites/default/files/PosInt7_Guide_comp.pdf ).
Also, some ideas about “everyday” number lines from the LMR curriculum (may or may not be familiar to the younger set): rulers, thermometers, numbered houses on street, graphs, race courses, and even CLOCKS! This makes me wonder if rulers/clocks might be a place to create a “need” for equally spaced tickmarks, because we need each minute to take the same amount of time. I’m thinking of a clock without any numbers or markings sitting on paper or a white board, and students could create markings using a stopwatch to time intervals of their choice. (<–not a fully formed thought, but maybe an interesting place to start)
Whoa! So many great thoughts and resources! Thank you, and I look forward to digging through the LMR materials. Fun, fun!
Yes, me too!
Amazing lesson! I think wonder if regular spacing would come out more naturally if you separated the tasks of numbering the points, and choosing where they go. If a group gets a sealed envelope with unknown numbers (maybe 4-14), and they’re asked to first decide where the numbers will go. Then they open the envelope and decide which number goes on which mark that they made. I think numberless marks might make them all look the same, so the feeling that they should all “get the same space” might come more naturally.
Interesting thought. Thanks! I did like having the kids choose their numbers, so I’d like to preserve that, but I think slowing it down and separating the parts would give the kids more chances to revise their thinking. I think we probably did too much in one day, just because of the constraint of me being there infrequently. I think the teachers may slow it down and really explore, and I can’t wait to see what they find out!
What a wonderful activity and all the reflection that went into it too! And all these great comments!
I like the question about equal spacing. And we know where you’re coming from. You don’t want to be saying, “Make me a number line.” They make theirs and you say, “Why don’t we change it and make it even better?” It was brilliant already.
( I had this on Friday when I got my Y4s to explain the eclipse. They did so well – http://y4ist.blogspot.fr/2015/03/the-eclipse.html – I could see their sun rays weren’t parallel, but I definitely wasn’t going to say, hold on, you could make your diagrams even better…)
It’s a feature of getting children to explore things and create things themselves isn’t it? What they create often calls more for appreciation than for improvement. And the great thing is you see what next step there might be, and, after a decent interval (weeks perhaps), you can start a whole new activity that involves, that needs even, this step.
This is what you’re saying about time isn’t it?
My main thought apart from this is also about appreciation. It’s brilliant that you’re documenting this for us educators. And the great number lines you’re installing all over are a monument to the children’s work, as well as a tool for thinking and playing. I wondered though if you blog it for the parents too? Or make a wall display with the photos of what they’ve done? Such good work should be shared with everyone!
Thank you, Simon, for your wisdom. That is what I was saying about time, even though I didn’t know it yet. Thank you for helping me know it.
Another thing, that is literally and metaphorically off at a tangent. I’d always thought that Euler’s formula was something I’d never get round to understanding (I didn’t do a maths degree). You know the famous one, e^(ipi) = -1.
But I saw a video this week, that, even though I didn’t understand it, made me begin to think I might grasp it solidly one day.
https://youtu.be/F_0yfvm0UoU?list=PLZHQObOWTQDOsm00wt1avh6FakzOdTzoO
What this introduced to me was the idea of *rotating* on the number line! It’s really bowled me over.
I love how there’s still movement involved, still an analogy to the body and the world we live in. And I love that something that I thought was probably a matter of complicated algebra and trig can perhaps be appreciated… after quite a few more steps… as something on our old good friend, the number line!
Your post is quite remarkable! Thanks for all the details and photos. You modeled the kind of reasoning (both for teachers and kids) which I think is the key to enjoying and learning math. I must reblog this!
Reblogged this on Teachezwell Blog and commented:
If you want to see teacher and student reflection and authentic engagement in math activities, read this exceptional post on creating number lines. I believe this is what we WANT to happen in schools. Very encouraging!
Thank you!
Tracy, I’m so excited to see what happens this morning when my kinders come back and revisit the lines. There are some amazing ideas posted here and I’m thrilled to be able to have such thoughtful and articulate comments to draw from. The rest of this year is going to be a unique and interesting exploration for all of us here in kinderland and I’m already thinking about the first day of school next year. Thank you Tracy, you are the best!
Becky, I am so lucky to get to come visit you and think and teach with you! It’s the best. And this is why I blog, right? Look at all these amazing ideas. I’m really into the rhythm one. What if they clap or drum as they walk the lines? Daphne and I did that in the car this morning with our imaginations, and she got a total kick out of it.
This morning, though, I’ve been taking a step back further. I’m thinking about why the numbers are spaced evenly. There are lots of ways to think about it. One thought was, if we’re counting by ones on the number line, then each time we go to the next number, we’re adding one. One stays the same size. Right? If we’re counting by twos, we’re adding two each time, and two stays the same size (within the scale we’ve picked for that number line).
I guess what I’m wondering is what do kids need to think about and figure out to decide for themselves that the spaces should be even? Not because of convention, but because of math?
Oh, another thought I had about revising the uneven ones. As kids decide to make changes, I think there are two really cool solutions that might come up. One is for them to peel up the numbers and scale them evenly. Another would be for them to leave the tape and change the numbers. Right? Like if it goes 2_3__4, what number should be where that 4 is? What if they decided to leave their tape where it was, and write 2_3__5? Is the 4 still there?
In practice, I think that would turn into a hot mess, and we’d have some fractional lengths, and all kinds of thorny issues for kindergarteners. But it would also be awesome. So, if kids think to keep the spacing and change the numbers (rather than keep the numbers and change the spacing), why not see what happens? They may not think that way, but I wanted you to anticipate it in case they do.
Kassia and I started to think about picture books that have even intervals/number lines. We’re coming up dry so far. Any thoughts? One metaphor that Maya had us thinking about are stepping stones across water, like these photos: https://www.google.com/search?q=river+rothay+stepping+stones&espv=2&biw=1164&bih=561&tbm=isch&tbo=u&source=univ&sa=X&ei=OBkQVbfvC7TLsATntoLoDQ&ved=0CB0QsAQ#imgdii=_ Is there anything that would work down at Salmon Falls? The train trestle, the bridge, spindles on the bridge railings? Or another walkway across the water? Given the role of the river in town, maybe there’s something there?
What about the train tracks??? Not that I’m saying to have the kids play on train tracks. But, you know, I did as a kid. We walked along them, jumping from board to board. Is there a safe way to think about the train? Also, we didn’t really take up your telephone pole idea, but why not? Is there a stretch where they’re evenly spaced? How fun to get kids looking at different scales…
Becky, I just had another thought. Remember how we started with the chart, and they told me it wasn’t a chart, it was a calendar? Maybe we can go back to that meaning? The school day is their unit. And each school day is the same size (more or less, right? Or are there early releases?). There aren’t tiny school days and then huuuuuge school days…
Just a guess from my own rural upbringing, but maybe the kids in your class do have a familiar number line context: playing with the measuring tape their parents use for DIY carpentry projects at home. Or, a similar tool for sewing projects.
This is such an interesting lesson and conversation! I really appreciated what Graham said about the abstract nature of the task, and wanted to add another resource, which is that John Van de Walle says that number lines are “not recommended” for students below third grade. According to him, they are too abstract and if you do use them, you should emphasize the concept of length — so instead of pointing to 5 and saying “this is 5,” draw an arrow from 0-5 and say “this much is 5.” I have often drawn numbers on the ground and had kids use them to count their steps, to emphasize the distance concepts embedded in the number line.
Now, I don’t know if Van de Walle is right — I’ve had many second graders use the number line quite fluently to solve addition and subtraction problems. And I know you are just introducing it as a way for kids to explore a new idea, rather than for mastery. I just wanted to mention his caution because kindergarten is really young for us to expect mastery of these abstract ideas, and I think it’s important to emphasize that to avoid teachers pushing kids too far, too fast.
Heidi, thank you so much for this comment! I need to read up in my Van de Walle. So interesting! You might enjoy this paper that I found the other day: http://lchc.ucsd.edu/Festschrift/Library/Numberline-n-Measurement.pdf Gets at some of the developmental stuff. Today, I was in a second grade, and a couple of the kids clearly didn’t have the “equal interval principle.” Uneven intervals didn’t bother them a bit. Meanwhile, other kids were all about making them exactly even. I was happy to let them explore, and wasn’t at all worried about mastery.
NUMBER LINES! I happen to be working on a research study right now on the development of the open number line. The context I use is measurement with cubes (Measuring for the Art Show by Contexts for Learning). Using connecting cubes to measure distance works well because the kids fill the entirety of the space, thus connecting the idea of iterative units (the cubes) to a total length from zero to whatever. They just have to measure something that they actually care about how long it is. The unit goes into addition, but you could explore a measuring context. It is fun to give kids two colors of cubes only, and then encourage kids to design their own measuring sticks, and seeing what patterns emerge (groups of 2, 3, 5, and 10).
http://www.amazon.com/Measuring-Art-Show-Addition-Mathematics/dp/0325010102
Wow, Rachel! I haven’t read Art Show, but I love me some Contexts. I need to pick it up. 🙂 When the kids use cubes, what have you noticed about the kids’ intervals? Similar to what we noticed? Specifically, how does the idea of equal intervals come up, and what convinces the kids equal intervals are important?
I saw an article study on how Chutes & Ladders helps kids learn the number line & did some searching. There’s another game that helps kids learn how the number line works, incl negative numbers. https://amazingwizkids.com/product/escape-medusas-rage/
I think a lot of kids who are visual learners and/or kinesthetic/spatial find it easy when they can see the numbers and use a manipulative.
I’d love to hear if kids like playing it!