Maya (7) brought home a folder full of completed math worksheets yesterday, which put me in a funk. First, there was the bugs problem.
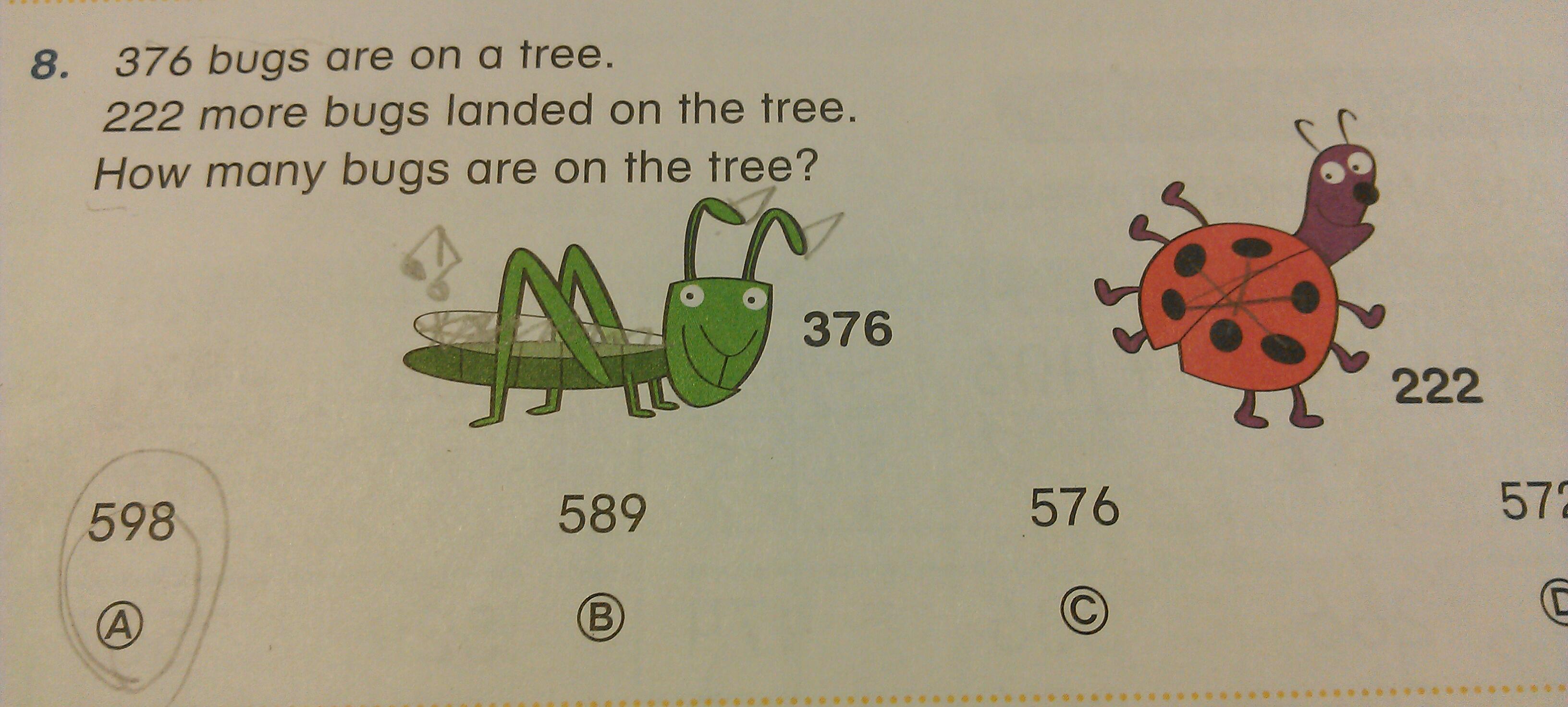I couldn’t decide which part of this problem bothered me most. Was it the ridiculous premise? I mean, come on. Was it that the problem was, yet again, a multiple-choice question? Was it the stubborn insistence on drawing bugs with the wrong number of legs? Was it that students have no room to work, but the publisher took plenty of room for cutesie drawings? Harumph.
As awful as the bugs problem was, the page that really upset me was this one:
Sigh. A few issues:
- The strategies are named wrong, and made to look more complicated than they are.
- There are better and other ways to solve this problem.
- Students are left with 2″ to do math on this entire page, which is barely enough room to do the standard algorithm. There’s no chance they’ll try out one of the other strategies with no space to work.
- Once again, we’re turning useful, general computation strategies into prescriptive algorithms. Breaking the numbers up by place value and adding the partial sums becomes: Step 1) Add hundreds…
I’m not the first math teacher to notice that prescriptive worksheets are a problem. Kamii, the CGI group, and others have all written about it. Yesterday, though, I was upset as a parent because Maya has stellar, flexible mental math skills, and her instinct to think is being undermined by this curriculum. I asked her why she’d opted for the standard algorithm on all the problems, and she said, “Those other strategies are too confusing.” I covered up her solution to 597 + 122 and asked her to solve it mentally.
“Well, I’d give 3 to the 597 to make it 600. Then 600 + 122 is 722. I’d take the 3 back, so it’s 719.”
I did the same thing for 209 + 376:
“200 + 300 is 500. 500 + 70 is 570. 9 + 6 is 15. 570 + 15 is 585.”
I pointed to the top of the page and said, “You just used this strategy. You broke the numbers up into place value parts, and then added each part together, starting with the biggest part.”
Her jaw dropped.
And my mind clicked. She has made NO connection between the mental math strategies she uses with fluency and all this junk on the worksheets. The reason? She’s never been given the chance to record her own thinking at school.
I think I’ve decided what one of my bigger problems with this curriculum is: they never use blank paper. They never write 209 + 376 at the top of a big piece of paper and let kids have at it. The kids never get a chance to wrestle with keeping track of their thinking or figure out organizational strategies. All math problems are either on worksheets or educational technology. The kids just don’t write enough.
So now I know what to do with Maya at home. We’re going to spend some time with blank paper, where she has to work out how to write down what she does in her head. She needs to make mistakes, lose track, not be able to follow her own thinking, and then ultimately figure out ways that make sense. She needs to be able to write down her thinking so that she and her mathematical community can follow it. I’m on it.
Two hours later, after dinner, Daphne (5) got us started. Our dining room chairs have decorative nailheads, and the kids are forever running their fingers over them and counting them. Daphne said, “Someday, I’m going to get out a math journal and count all these nailheads and write it down so I know how many there are.” Before I knew it, she was off! Someday turned out to be right then. Both kids got in the game.
Daphne was incredibly excited to count AND write down her results. Check them out:
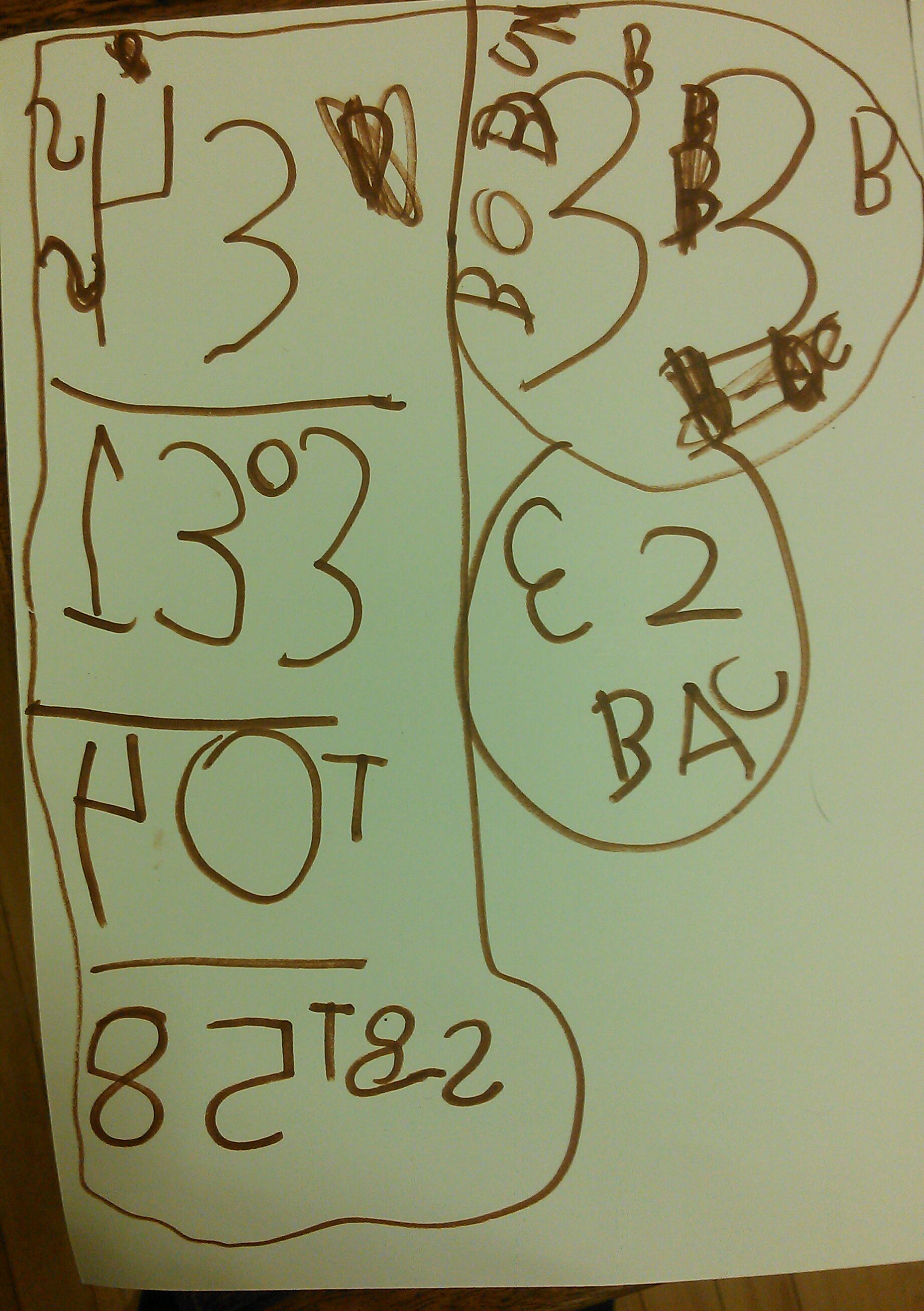If you want to understand her notation, take a peek at the short videos:
The power of blank paper, baby.
Perhaps inspired by all of this discussion and my venting, Maya asked if she could get a piece of blank paper when she did her homework, which is truly a counter-cultural act with this curriculum. “Of course!” I nearly sang.
She created this number line and used it to solve the final problem.
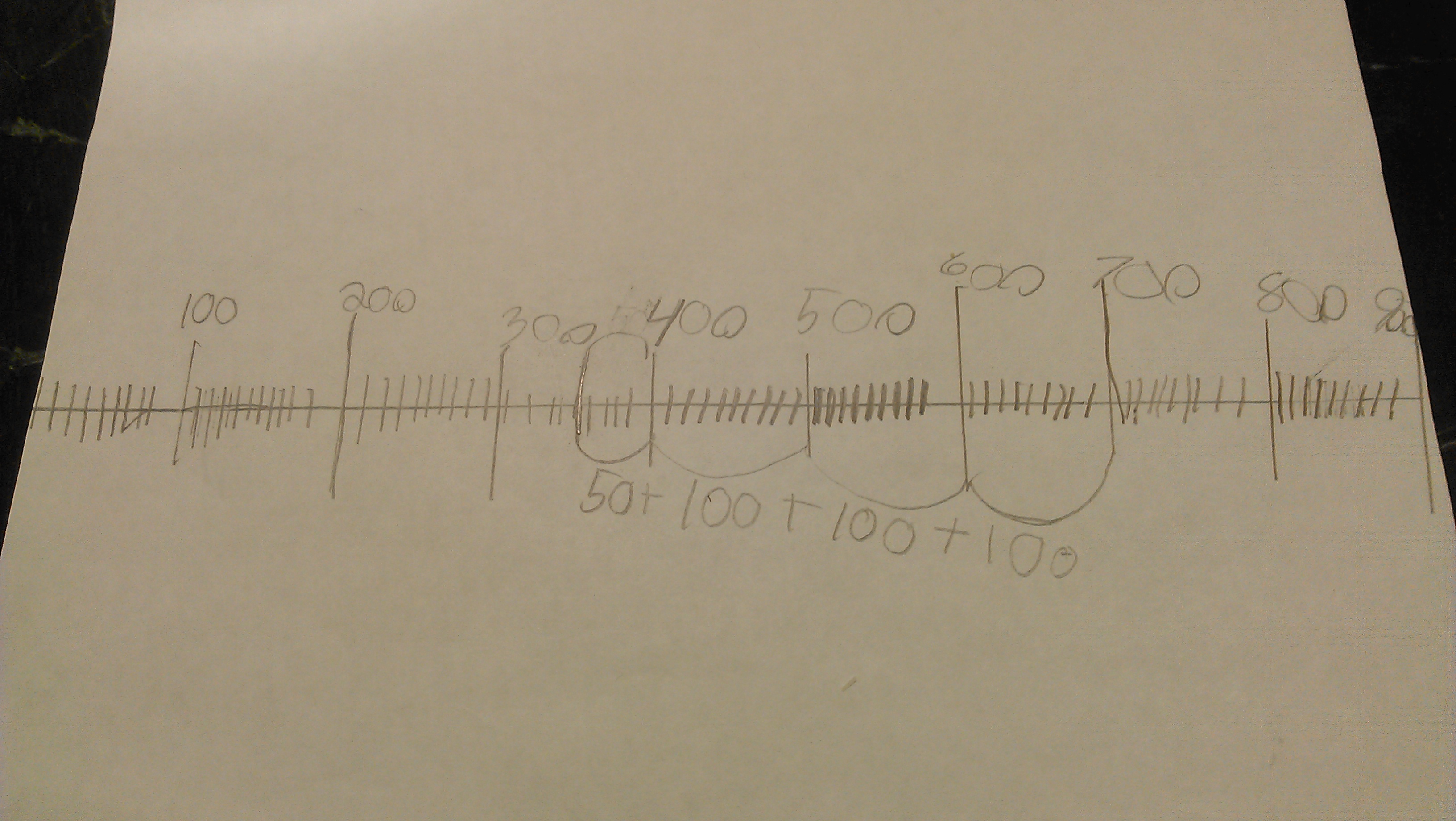When I asked her about it, I pointed out that she didn’t just answer the question by saying, “The red one.” She wrote about the problem more generally: “I used a number line and found that anything less than 350 would fit and 270 is less so red paint is less than 350!”
She said, “Well, when I wrote it myself I thought about it more.”
Precisely my point.
Thank you Tracy for your wonderful insights and posts. I’m sharing them with the elementary teachers at work. They are inspiring.
Thank you, Teresa!
This sounds awfully familiar! I have grown to hate opening my kids’ folders on Wednesday when they bring them home – full of worksheets with no room for their thinking.
I still can’t believe that packet you photographed. We’ve lost our minds.
I really enjoyed reading this post. I teach middle school math and found it so interesting to read about how early the problems of math education appear in our schools. I had never really thought about how the lack of space on the page would effectively stymie mathematical thinking and would in effect place much greater value on the right answer rather than the thinking needed to arrive at the answer, let alone multiple strategies for solving problems. No wonder I have to spend a good chunk of my time reminding students to SHOW YOUR WORK!!
I love this comment! Yes! I agree completely! For my daughter, every representation is provided and every procedure is spelled out. She has no idea what “show your work” means! This curriculum is all about answers. Kristin Gray (@mathminds) pointed out on Twitter that the teacher gets NO useful information from these worksheets. Right or wrong answers. Nothing formative or informative she can use to plan instruction. My focus in this blog was the effect on the learner, but holy mackerel, these worksheets aren’t working for anybody involved.
1: I am sure that Mr. Pearson uses a calculator to find the answers.
2: Now that all the money has been spent on computers and tablets and jolly worksheets there’s none left for parer and pencils.
3: I cannot agree more. Maths needs paper. It needs a waste bin. How can one think without some means of SEEING what you are thinking about.
Amen.
I’m going to ask my kids what they think of the bug question tonight.
Blank paper seems to be something I’ve gotten half right in our little math class. We give homework assignments that the kids write out themselves on their own collection of blank paper. I had a momentary observation that it was interesting to see what different results come back ranging from draft work all in a jumble to polished versions that were clearly a second (or third) draft. What I failed to do, until now, was realize that we could talk more explicitly about the structure of what the kids wrote to help them make sense of what they were doing.
One other observation; something about the worksheet structure de-cues the use of manipulatives. The second worksheet example even has a perjorative “use models, if needed.” I don’t remember ever seeing a child look at a worksheet problem and then get out their blocks/cuisinaire rods/ten frame/etc without being prompted by a teacher. I guess it happens in some classes where they have already created an extremely strong habit for using manipulatives?
Also, way to remove meaning from the word “explore” (as in “Exploring adding 3 digit numbers.”) What are some real explorations? Maybe:
– If you add two 3-digit numbers, can you get a 1-digit answer? 2-digits? Why?
– How many digits can you get in the final answer when you add two three digit numbers? What if you add three 3-digit numbers? Four or more?
– What is the most 3-digit numbers you can add together and still get a 3-digit result?
– Take any 3 digit number. Reverse the digits (e.g., 358 -> 853) and add the two numbers. Do you notice any patterns?
– 1089 trick: 3 digit number with distinct digits, reverse and subtract the smaller from the larger, then reverse digits and add. What do you find? Why does this happen?
– Using 3 distinct numerals, how many 3 digit numbers can you make? Add them all together. Try with another starting set of numerals. Notice any patterns?
– (older kids?) If you add two randomly chosen 3 digit numbers, what is the chance the sum is a 3 digit number?
– (meta question) What ideas do you have for exploring?
Finally, what would you do to help out the poor teacher who is the proximate source of these worksheets?
So many good thoughts here. Agreed about the misuse of “explore.” Same goes for “models,” by which they actually mean “algorithms.”
I think it’s a great use of classroom time to look at different students’ strategies for recording their thinking. Were they able to keep sense of the problem throughout? Can other people follow their thinking? Do the representations match the strategies? Students pick up useful strategies from each other that way.
As for the teacher, I’m trying to support her, and the school, as constructively and positively as I can. It’s very hard to be a teacher and a parent!
Talked about the bug question w/ my 7 yo tonight. His first question: why do they have those choices, why not just a space for kids to write their answers?
Maya has asked me the same question many times!
My 5 yo had this proposed salvage: for each choice, what can you change about the question so that choice becomes the correct answer?
Nice.
Tracy, this is Beautiful! I love how your children made a math journal to solve a natural problem that has been stewing in their brains for a while. When considering “homework” or even classwork, I’ve always believed in the premise of “the more white space, the better.” You’ve taken that to the extreme and as I mentioned at the beginning, it’s beautiful. Thank you for sharing how your children lifted you out of some math doldrums that, as parents, we all experience.
Thank you so much, Mike! I’m totally with you on “the more white space the better.”
I love the name “Becoming the Math Teacher You Wish You’d Had”, and it makes me want to start another blog “Becoming the Math Teacher You Want Your Children to Have”. It seems almost every day I have to decide whether to provide homework help that aligns with what the assignment actually is, or provide the help that is more disruptive, but also conveys what I really want my kids to learn. I’m currently blogging at https://mathisforeveryone.wordpress.com
Thanks so much, Nancy. I’ll add it to my reader! And I share in your struggle…
As a teacher of this program, I completely relate to your concerns about space to work and prescriptive algorithms for flexible thinking! I have my students start with Number Talks, agree, disagree, and pose lots of strategies. I find that helps. I also have students work out problems on white boards. In second grade, they still love it and use it as a tool more than scrap paper. But I find the assignments very poorly designed overall. From a teaching perspective, where, in my school, I must use the program as my main instructional guide, the frustrations are shared with your parental concerns!
On another note, I’m really enjoying your blog! Please keep these great reflections coming!
Thank you so much for this comment! I’ve thought a lot about how I’d handle it if I needed to teach this curriculum, and I’d be taking the same approach you are! Number Talks, white boards, discussion, etc. When the kids are supposed to practice 12 identical problems on those colored 4-pagers, I’d be picking out the 3 problems I like best, recycling the worksheets, deleting the scaffolding, and giving the kids a crack at making sense of the problem for themselves!
“She has made NO connection between the mental math strategies she uses with fluency and all this junk on the worksheets.”
I think this is huge. Since about two years ago, this is something that I have noticed and have been thinking about. My hypothesis is that this generally happens because a teacher presented computational strategies- “presented” being the important part. By presenting them, as you noted, the strategies become step by step algorithms in the minds of many students. Then, when students try to solve computational problems, they try to apply them instead of thinking the way they naturally would think about it. They’re trying to follow Mr. or Miss/Mrs. ‘s strategy.
I think one way to counter all of this hapenning is to represent and note student thinking often, publicly and visibly for the whole class using a format such as Number Talks (or something along the line of Number Talks), especially in the first third to half of the school year. By posing a computational problem and asking to students to solve it mentally, they almost have no choice but to use what they are comfortable and fluent with. By then accurately representing and noting student thinking, we are providing written models of their own thinking. “When I think this, it looks like that on paper” To me, that is the key to all of this. By doing this often, students will have lots of practice seeing what their thinking looks like in mathematical notation and, for having a teacher say this to me, will eventually transfer this to paper.
ps.- I can’t believe you took a jab at the friendly, smiling, colourful, bugs. Sheesh. 🙂
I love this comment so much, Pierre. Agree, agree!!
Math has certainly taken a new direction!
Informational video!