Last week, between work with grade-level bands, I had a complete K-6 staff for about an hour. I wanted to tackle “story problems,” so I started by showing them “How Old Is the Shepherd,“ by Robert Kaplinsky:
Seriously, take the 3:07 to watch it. You’ll see that 75% of 8th graders presented with the nonsensical problem, “There are 125 sheep and 5 dogs in the flock. How old is the shepherd?” answered with a number.
I had given my close friend and colleague, Debbie Nichols, a sneak peek at the video. She often helps me think things through, and is one of the teachers I am profiling heavily in my book. She decided to give the same problem to her 1st and 2nd graders to see what would happen. We both expected the younger kids to do better on the nonsense problem, mostly because they haven’t been trained to pluck-numbers-and-do-something-with-them the way the older kids have. In our experience, younger kids are great sense-makers.
Debbie changed the problem to read, “There are 25 sheep and 5 dogs in the flock. How old is the shepherd?” Partway through, she wondered about vocabulary, and added a second question, “There are 25 kids and 5 dogs in the classroom. How old is the painter?” Debbie interviewed her students individually, recorded it on video, and sent me her notes with the subject header WOW:
| Response to sheep version | Response to painter version | Grade |
| Is this times or add? I have no idea. I do not get it. 33? | 2 | |
| 37? I thought, my mom is 37, so he might be 37. I was going to try to count to the highest number and then count on with the other number. I was gonna try to but then I changed my mind. Or I could just do that number and then count on. | 1 | |
| 7? I don’t really know, because I’m guessing. What’s a shepherd? | 2 | |
| A shepherd? 5. I just, I don’t really know. I’m just really good at it and I like animals. | 1 | |
| 11. I’m trying to hold numbers in my head and I just counted. | 20 years old? | 1 |
| I know 25 + 5 = 30. | 30 | 2 |
| 25. You said 25 sheep. | 25, because you said 25 kids. | 1 |
| 30, because I added them up. | 30 | 2 |
| 25. I was just thinking. I was counting. 30? | 32 | 1 |
| Shrugged shoulders. 30? 32? | 7. I thought of the question. | 2 |
| 8. I was counting. | 8. I counted by 9s. | 1 |
| 8. Is that correct? I thought it was a little boy so I chose 8. | 20. I thought of another number. | 1 |
| 5. I just got it out of my head. | 20. It just came out of my head. | 1 |
| What are flocks? What’s a shepherd? 29? 59? | 69? I got it out of my brain and my brain is made of pink worms. | 1 |
After individual questioning, Debbie brought the kids to the rug and asked the whole class, “There are 25 sheep and 5 dogs in the classroom. How old is the teacher?” Students quickly fell in line behind some opinionated students, and came to consensus that the teacher was 30 because 25 + 5 = 30.
Wow indeed. What’s especially striking to me is how many students admitted they didn’t understand the problem, and still gave a numeric answer anyway. Some of the nonsense answers even sound kind of right–like they are imitating the way a math answer should sound. “The answer is 8. I counted by 9s.” (As much as I love the brain made of pink worms, the counting by 9s answer is the most fascinating one to me.)
The following day, Debbie posted, “There are 4 kids and 3 chickens in the room. How old is Mrs. McCabe?” (Mrs. McCabe is another teacher in the building.) Students wrote their answers on the chart paper. Take a peek:
43, 7, 7, 40, 64, 70, 2, 2, 10, 9, 30, 36, 100, 34, 7, 44.
Nobody wrote, “I can’t tell because this problem makes no sense.”
43 and 34 come from students taking the 4 children and 3 chickens and using them as digits in a new number.
7 came from students adding the 4 children and the 3 chickens.
I suspect 70 comes from a student adding the 4 and 3, then deciding 7 was too young, so they made it 70.
40, 64, 30, 36, and 44 may come from students disregarding the information in the scenario, and just making a reasonable guess about Mrs. McCabe’s age (56). The 40 and the 30 might be similar to the 70, in that the numbers 4 and 3 were in the problem, and they were clearly too young, so 40 and 30 sounded reasonable. (In this group of answers, if students were thinking about reasonable ages for teachers, that’s something to build on. My next step would be to ask them for evidence in the question.)
2, 10, 9, and 100 remain mysteries to me.
I can see in the anchor chart that Debbie took out her purple marker and tried to help students recognize the lack of relationship between the number of chickens, the number of children, and Mrs. McCabe’s age. She had them try to come up with a question that would make sense from the chickens and children, like how many legs are there?
After reading Debbie’s notes, I wondered what my own children would do with this problem. I asked my 5-year old daughter, (who asked to be called D), “There were 4 children and 3 chickens in a room. How old is the teacher?”
“9.”
“Where’d the 9 come from?”
“No, wait, that’s not enough. 90.”
“Where’d the 9 come from and where’d the 90 come from?”
“Well, I added the 3 and the 4, and that made 9. But that’s not enough. Like, Maya is 7, and that’s 2 years less than 9, and she’s not old enough to be a teacher! So I made the 9 a 90.”
“Can you show me how you added 3 and 4?”
She counted on her fingers.
“Oops. It’s not 9. It’s 7. So she’s 70.”
I was quiet for a while, thinking about a question.
“We have 2 dogs and 1 fish, right?”
“Yeah.”
“So, we have 2 dogs and 1 fish in our house. How old is D?”
She laughed uproariously. “Mommy, that doesn’t make sense! The dogs don’t have anything to do with how old I am! 2 and 1 is 3, but I’m 5!”
“Really? OK. Let me try again, then. We have 2 dogs and 1 fish in our house. You are 5 years old. Let’s say we bought another fish. How old is D now?”
She was hysterical at this point. When she calmed down, I said, “OK, let’s go back to this question again. There were 4 children and 3 chickens in a room. How old is the teacher?”
“OH!”
I recognize that these nonsense word problems are contrived. I think they’re revealing, though. In particular, I think they show some problematic beliefs our students have about doing math:
- All math problems have to be answered with numbers.
- All math problems can be answered.
- It’s normal for math not to make sense.
Where do these beliefs come from?
In the last week, as I’ve been mulling all this over, I’ve been revisiting some of the books I have about the intersection of reading comprehension and math, like Comprehending Math by Arthur Hyde, Mathwise by Arthur and Pamela Hyde, and From Reading to Math by Maggie Siena. This quote of Siena’s about the foundations of reading jumped out at me:
“Children must…expect the things they read to mean something and expect to be satisfied by that meaning” (17).
Do we teach the same expectation in math? Or do we teach students to answer every problem with a number, guessing if they must, and it’s OK if it doesn’t make sense?
I’m still scratching my head over where this message comes from with my kids and Debbie’s students. D has grown up during the writing of my book, when I am hyper-aware of the math messages I am sending and hearing. Debbie’s students had a great year of kindergarten with a teacher who emphasizes making sense, and now they’re with Debbie, who teaches math for understanding. And yet, 100% of them answered the nonsense question with a number.
As a fan of CGI, I know children are naturally sense-makers. But I also know that reading mathematical problems is a special kind of reading, and students need instruction in it. Historically, teachers have used two different types of instruction for reading word problems:
- Teach students to “decode” math problems with “keywords,” like “in all means add.”
- Teach students to recognize unnecessary information, red herrings, and traps that “they put in the problems to trick you.”
On keywords, some of us have been having fun over on Twitter, creating a list of problems that show why it’s a doomed strategy. For example, Tommy buys 3 bags of avocados. There are 4 avocados in each bag. How many avocados did Tommy buy in all? Hmm. I thought in all meant add?
As for focusing on the traps “they” are putting in the problem, I am no fan of this strategy either. What sort of message are we sending kids with this teaching? That there are rooms full of nasty adults, rubbing their hands together, trying to set traps that catch nice little children taking math tests? Ahem. Though there may be some truth to that image, I refuse to cede mathematics to the standardized-test and curriculum writers who write crappy, trappy math problems. I want to snatch math back, and teach students to see the beauty and usefulness of math around them, and to enjoy the journey through a perplexing, puzzling problem. So red herrings and tricks be damned!
What do we do instead? How do we teach students to read math problems for understanding in a way that will yield empowered students who expect to make sense? I’m looking for resources on this question, so please pass them along in the comments. In the meantime, let me share three of my favorite approaches. They all have something in common, which is that they are all strategies to make it impossible for students to leap right to answering the question. All three approaches force students to slow down and make sense, first.
1. The Math Forum at Drexel University is a fantastic group of people who are all about teaching students to make sense of math. One of the strategies they have been promoting is Notice and Wonder, where teachers share a scenario without a question, and ask students what they notice and wonder. You can read about it in Max Ray‘s Powerful Problem Solving, by following Annie Fetter, or at a whole bunch of sites here, here, here, here, here, here, and here.
2. Brian Stockus wrote a great blog called “Numberless Word Problems,” in which he described a co-worker removing the numbers from a word problem. Again, this strategy eliminates the option of racing to an answer, and introduces students to the idea that we can do quite a bit of mathematical thinking about quantities without knowing what they are, which Kate Nowak framed as the the rich idea at the heart of algebra:
 3. In Mathwise, Art and Pamela Hyde wrote, “Getting students to slow down and think about a problem is not always easy, especially if they are used to calculating answers quickly to one-step translation problems. We have found that students can be encouraged to think through their assumptions with an intriguing type of problem called “Fermi questions'” (66). Fermi Questions are mathematical questions where answers seem impossible, but we can get close by making some assumptions and then approximating:
3. In Mathwise, Art and Pamela Hyde wrote, “Getting students to slow down and think about a problem is not always easy, especially if they are used to calculating answers quickly to one-step translation problems. We have found that students can be encouraged to think through their assumptions with an intriguing type of problem called “Fermi questions'” (66). Fermi Questions are mathematical questions where answers seem impossible, but we can get close by making some assumptions and then approximating:
- How many piano tuners live in Chicago?
- How many kids could fit in the gym with no furniture inside?
- How many hairs are on your head?
From a teaching point of view, Fermi Questions can be fantastic for helping kids realize they are making assumptions and connections and using their prior knowledge in mathematics.
All three of these strategies–Notice and Wonder, Numberless Word Problems, and Fermi Questions–force students to slow down and make sense of the situation before worrying about the answer.
I’m hoping to learn more about high quality instructional strategies for math teachers that are rooted in what we know about teaching reading comprehension. Annie Fetter presented on this idea at NCTM in New Orleans, and I think it’s an idea with long, strong legs. The connection between making sense in literacy and math is something I talked about in the workshop last week, and it seemed to resonate with Shawna Coppola, a wonderful literacy specialist. I loved her notes:
Making sense is the thread that ties everything together, in every content area. Right? If our students arrive having already internalized the message that making sense isn’t part of math, or that math doesn’t make sense, or that word problems are just a bunch of numbers hidden in words and traps, we have our work cut out for us. Time for some intentional, creative, inquiry-based teaching that empowers students to make sense.

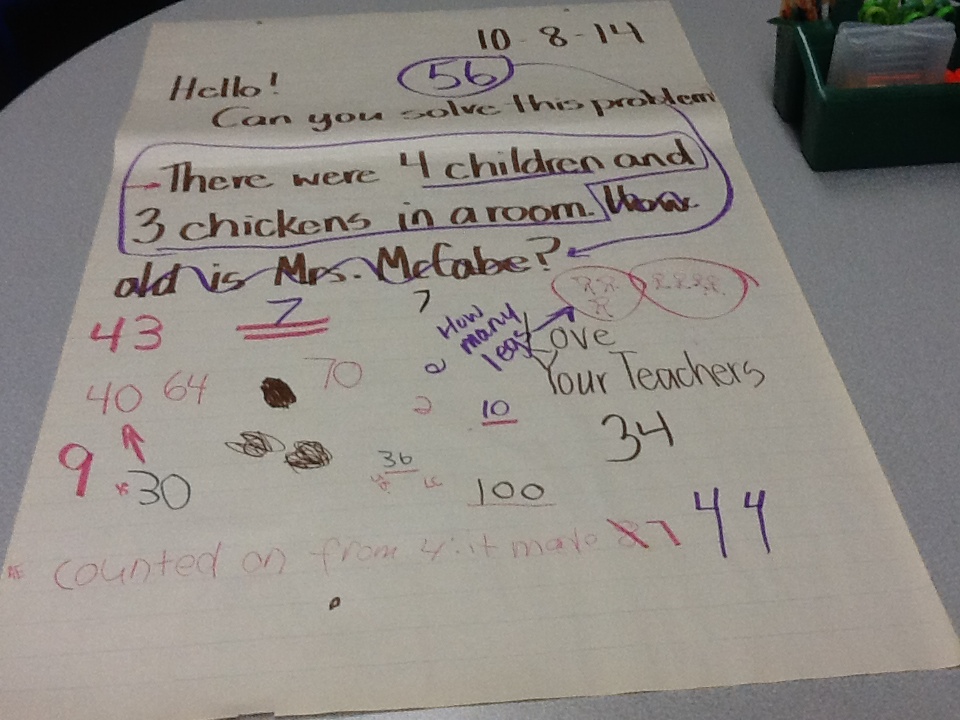

This is such a fantastic post. I need to process it more, but my first thoughts are:
* Fermi questions sound terrific for modeling with math as well as for making sense of problems.
* 101qs.com and three-act problems could help a lot with thinking about what kind of problems we can investigate (and how) from certain information.
* A possible first step would be to set up a scenario and list some questions to consider, then ask students which ones we have enough information to solve (and make it more than one but fewer than all). The problem is this seems to promote the idea that it’s normal for math not to make sense (teacher gives nonsense questions), but I think it could be taught as something that promotes critiquing math ideas.
* I admire how neutral Robert Kaplinsky was in that video, but it kind of breaks my heart the way the ones who realized it was a nonsense question don’t seem to feel good about it. I want to interrupt and yell “THAT’S RIGHT!” You don’t get the impression they feel safe and confident critiquing the question. I let students mock word problems if they can come up with a sensible, smart objection (“Why does she have to use up all the granola bars and apples? Can’t she just save some for later?”). (Then we usually solve them anyway because it’s pretty tough to come up with a GCF word problem that does make sense.)
* My spouse & I immediately wondered if the kid who answered “42” was a smartass Hitchhiker’s Guide fan who actually got the joke.
Julie, thanks for commenting! I am right there with you about the students’ lack of confidence, conviction, satisfaction. It’s harder to measure, but students’ affect about math is something I’m looking for all the time. I want them to OWN it.
I have been working with a teacher who has students talk about whether the math makes sense every. single. day. The difference is amazing. My favorite moment was when a student was explaining his thinking, then stopped partway through and said, “Is that right? Does that make sense?” Rather than looking at his teacher, he looked down at his own whiteboard. Everyone was quiet, waiting. And then he said, “Yeah, that’s right.” Kept going with his explanation.
Best moment ever.
Tracy, I think your wish of having students “OWN it” is key! A few years ago I used the phrase “Unsilence Students’ Voices” when I wrote a journal article and then I used it as the title of my Ignite talk. One of the key ideas of helping all students’ find their voices is the idea of having them “own” their thinking. Even if kids are encouraged to make sense of things whether it be a story or a math problem or how to organize a game, if an adult takes over (rephrasing their thinking or other strategies that seem to be helpful but instead are taking back ownership of the “problem” or “task”) then I think the result is that the student doesn’t feel like it’s “their” problem or “their” work. I wrote or talked a little more about these ideas here:
Owning It
http://mathforum.org/blogs/suzanne/2013/08/04/owning-it/
Learning from Watching
http://mathforum.org/blogs/suzanne/2013/04/05/learning-from-watching/
Unsilence Students’ Voices
Ignite: http://www.youtube.com/watch?v=QZrlQBraxwY
Article: http://mathforum.org/articles/communicator.article.sep.2012.pdf
~Suzanne
I regret not following up with the kid who replied with 42. Would have been amazing if he came up with that reasoning for his answer.
Maybe they read the Hitchhiker’s Guide to the Universe…(couldn’t resist).
I see the problem as a result of the rush to symbols. How much time is spent talking about numbers, doing simple operations in the head, or with bricks, or pictures? Nowhhere near enough. Far too soon the kids are writing 2+3=5, and hopefully understanding “number bonds”. How long is spent on talking about “number problems” without reference to things?
A kid with no formal schooling would not fall into the traps described above.
“Oooh, it’s a math class, there must be an answer”.
“Write a number sentence” is a death knell to common sense and understanding, when asked too soon, as appears to be the case………….
And the same goes for fractions.
Interesting. I thought something similar. But then my freshly minted kindergartener, who does a ton of meaningful talking math with me without early symbols, who is in an outdoor-based, totally informal school, who makes great sense of reasonable problems? She fell for it. I’m not so sure it’s that simple.
My opinion on the major misconception here? Students are taught at a very young age that all school math problems have answers.
I agree, that’s a huge problem. What was interesting to me, here, was that I asked the question of my kids while driving somewhere fun, totally not in a school setting, and still got answers.
My older daughter spends much of her free time playing around with deeper mathematical ideas: questions that have multiple answers, or no answers. But she answered the shepherd question with a nonsensical answer anyway. Three times since, she’s come to me and said, “I don’t know why I answered that crazy question!” It’s troubling her. I wonder if she’ll figure out why. Hope so.
My niece answered 30 at first as well. She is 8 years old.
Then I changed the question to, “You have 20 dolls and 5 cars. How old is your grandma? ”
Then she giggled and said that was a silly question. She then understood that her answer of 30 made no sense.
I am going to give the same type of question to my 4 classes of math 8s and 9s next week.
Thanks!
If you remember, will you report back? I’d love to hear how it goes! Thanks!
This is an interesting topic. A few years ago my district purchased an elementary math resource where the answer could be written in numbers, words, symbols, or not enough information (NEI). Some of the questions actually had an answer of NEI, but I found that students would rush to this answer if they didn’t know how to complete the problem. We don’t use this math resource anymore, but I always thought that having an NEI as a choice seemed to benefit students at some level.
Oooh, I like that…
A fix for overuse of NEI is to get those who choose it to either:
(a) explain what information they would like to have to answer the question; or
(b) show that there are multiple answers consistent with the information that is given.
However, I’m not entirely sure either of these would work for the shepherd’s age problem.
I recently used this problem again with a class of 6th graders. After giving them time to think about it and write their answers down, I recorded them on the board. The first answer was 25. The second one was something like, “This is a trick problem.” Admittedly, I was a bit frustrated that someone had given away the punchline so quickly.
Nevertheless, after recording an additional 10 answers, I had students vote. About 60% still picked 25. Then we had think-pair-share time and the people who thought it was ridiculous tried to convince everyone else. We revoted. About 50% still picked 25. Then we did another think-pair-share and still we got plenty of 25’s. Then I said that “I have two cats and one child, how old am I?” I got answers similar to those mentioned in this post where I was 3, or 21, or 12.
It was amazing to me that as many times as I have done this with kids, I still went from frustrated that the punchline was given away to amazed that they still didn’t realize it was the punchline.
Great post and thanks for sharing this.
Robert, that is stunning! I am amazed so many kids were unconvinced after several rounds of discussion and argument.
And I am equally stunned about the two cats and one child question. I would have thought sixth graders would see the impossibility of three as a father’s age. I’m sure they would if you asked them directly, but they’re not running their answers through that common-sense check.
I’m left with my questions, really. I had assumed kids went with nonsense by middle school because of what we’ve taught them about math. Now that I have preschoolers and 1st graders going with nonsense too, I have to revisit my assumptions. What’s the root cause? I’m not sure.
Thanks so much for your original blog and video!
This is so fascinating! I would love it if folks reading this post would try my sense-making experiment. The premise is that if we ask kids a math question, they do this sort of “pick out the numbers and do something”, whereas if you give them the same exact types of situations and instead ask them to draw a picture, they will step back and do the sense-making that they won’t do if they think it’s math. More at http://mathforum.org/blogs/annie/2014/09/16/join-my-math-and-sense-making-experiment/
I’m totally up for running this experiment in class Monday, Annie, but I think it will require changing Robert’s question. I don’t really want them drawing 125 sheep!
I have 3 sixth grade classes and 2 eighth grade classes. I could give the first class a nonsense question with the “draw a picture” prompt, and the second (and third, for 6th grade) classes the same question without the drawing prompt. There is a small risk they’d discuss it at lunch or something, but otherwise it would give a kind of control group.
I could do the 25/5 option instead of 125/5 (still kind of a lot of sheep), or I could make a different problem that might appear to tie into our current 6th grade topic, fraction division. Possible example: “It takes 1/4 cup of cocoa mix and 1 cup of milk to make a serving of hot cocoa at Joe’s Restaurant. How old is Joe?” or possibly end with “How many people ordered hot cocoa?” (harder to spot nonsense). What do you think?
I’d be having them do it silently on individual whiteboards, then sharing answers with a neighbor without changing what’s written, then talking as a class (kind of like in Robert’s comment). I guess my fear is that only a few kids would “fall for it” and would feel publicly exposed and stupid. But after everything I’m reading, that doesn’t seem very likely.
Aha! I just realized, in my experiment I can collect the individual whiteboards while they verbally discuss with a partner, then line them up at the main board by answer type. That way it’s not so obvious whose answer is whose, reducing the “exposed as stupid” feeling.
Speaking of sense-making, when I start replying to my own replies, maybe it’s bedtime…
Actually, for my experiement, I’ve got a set of three “math” problems and three “drawing” problems that you would give kids. They are not nonsense problems (though they aren’t earth-shatteringly interesting, either), and do have answers. But kids’ treatment of the “math” problems sometimes doesn’t look any different from their treatment of the shepherd problem. You would give students the two sets of problems two weeks apart (the math ones during “math” time and the drawing ones any time that isn’t math…but two weeks later or so). Check out my blog post to read more about it and download the problems.
I can’t wait to hear the results of your experiment, Annie!
Cannot agree more with what you stated. This is the status of education in the schools. The entire mechanism of education has to change. I shared the video in my blog post too.
http://journeythroughchaos.co.in
Yes, this is a fascinating post, Tracy! You’ve found something that’s kind of paradoxical and intriguing for us teachers and educators. Good to get our minds working on how learning really works!
Some of your suggestions were things I hadn’t looked into enough yet. Thanks for all those Notice and Wonder links! N & W is definitely going to be part of what I do a lot more, and a lot more explicitly! I tend to avoid word problems – which I feel a little guilty about – but the R & W approach seems to give me a way of getting more light than heat from them!
I’ll maybe give a version of the question a go with my kids when I get back from hols. I wonder if they will do the same things?
Like you say, I’m not sure it’s simply a question of school habits of mind spoiling things; there’s maybe an element of willing-to-please, and perhaps a sort of impulsivity in this too?
I read something recently in Malcolm Gladwell’s “David and Goliath” that this reminded me of. There’s this test called the Cognitive Reflection Test. It just has three questions, questions which people often get wrong:
● A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?
● If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
● In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
The weird thing is that people do better when doing the test is made harder. Researchers Alter and Oppenheimer printed out the test questions in a font that was really hard to read— a 10 percent gray, 10-point italics Myriad Pro font – and scores went up!
Alter explained the finding by saying that the difficulty causes people to “think more deeply about whatever they come across. They’ll use more resources on it. They’ll process more deeply or think more carefully about what’s going on.”
Thanks so much for your thoughtful comment, Simon! I’d love to hear what happens if you try this out in your class. I’m hoping some people will try it out with N&W, or making it a numberless word problem, and then see what happens. Does that pause–where an answer is impossible and the student has time to think–make a difference? I’m especially curious if students will hold on to their conviction. Let’s say a student says it can’t be answered when there are no numbers in it. What happens when numbers are inserted?
I think you’re right about a desire to please, and impulsivity. Both must play a role…
I’m curious where you go with it. You always take ideas to new and exciting places!
Tracy
Well, we did try it today. I thought I’d make it more familiar in context: “There are 25 chairs and 5 tables in the classroom. How old is the teacher?”
I was surprised: everyone (30 children, aged 8) – everyone – gave me a numerical answer!
I asked them why they did this when the question didn’t tell them anything about the age. A typical answer was, “Well, the question had numbers in it, so we thought we had to do something with the numbers.”
I showed them the video – which they liked – to round off.
I find this result very thought-provoking, like a little occasion of the Emperor’s New Clothes, that we are so willing to “know” something. I know I get my class to do lots of imaginative things, like looking at a Paul Klee picture, A Young Lady’s Adventure, today and writing a story about it. They obviously have to invent a lot. So maybe that element of play and invention feeds in too?
Today while we were talking numbers one of my students remembered this question, and then another posed a similar question. I was really pleased the thought hadn’t gone away, and they were able to see that it’s another example!
A SQ1TV song says: “Think about the problem, then step back. Try a different plan of attack!”
One of the habits we should be teaching is, when they step back, to ask “what does the question really mean?”
For the shepherd’s age question, students seem to be triggered to think they are answering a “math-class” question (MCQ). MCQs have the following characteristics:
(1) they have exactly one single correct answer
(2) they can be answered using the tools you have been taught
(3) they require a mathematical object as an answer (e.g., number, shape, graph, etc)
(4) they are asked of students, not by students
(5) they require entering into an idealized world where you only have the information given to you within the question, no more and no less
To be clear, I am not saying these are desirable characteristics or that we should be emphasizing these in our classes, but I think they are the most common type of question in math classes and math exams. Of course, MCQs appear in other settings, too, particularly riddles/puzzles.
There is a lot of great work toward eliminating the connection between questions asked in math classes and my MCQ properties (1)-(4). However, I think the shepherd’s age data suggests that these are very deeply embedded and we have to recognize that it will take a long time to fully eliminate those assumptions.
Point (5) is, of course, common to a lot of good questions, too, and it is very subtle. Indeed, teachers commenting here aren’t sure when the students are using or not using their external data. For what it is worth, I personally believe it is important to give students a bias toward explicitly using their background knowledge whenever possible since this is a habit that will serve them well outside the classroom.
Finally, I will ask my children at home this question and I am sure they will give me numerical answers. The real test is how much they are giggling when they do so, because they love to give me silly answers, especially when they think the question is silly.
Oh, and my personal answer to the shepherd question is “older than 16 years and less than 90” based on:
(a) a lot of animals to look after
(b) the sheep alone I estimate having a market value around $40,000 (average 80kg/head * $4/kg * 125 head)
Both of these suggest to me that the shepherd is functionally very close to being an adult, but only 0.7% of the US population is over 90, so that’s just unlikely regardless of the number of animals.
Your list of 5 traits of MCQs is really interesting. Thank you! What was interesting to me was to see a kindergartener and first-grade students following the cues, even without much classroom experience. How did they get trained up on them?
I don’t seem to be able to reply below your comment, Simon, but I love that question!
Great post. I appreciate what you brought to the discussion! Definitely stealing something form this!
Thanks! Glad you liked it. I’d love to know what you do with it.
I know this comment thread is sleeping, but incase anyone comes across this later (as I did).
I asked my 4.5 year old (who goes to half day montessori program) a similar question using smaller numbers.
6 fish and 3 stuffed animals at the library, how old is the librarian ?
She gave me a goofy grin and answered “9”. When I asked her how she came up with it, she demonstrated counting up on her fingers.
Tracy,
I loved reading through this post and the comments! I am reinventing a presentation I gave a few years ago for the upcoming NCTM Annual 2018 conference and your post, twitter thread, and Robert’s videos are invaluable for upgrading my thoughts. Thanks for sparking such invigorating content for teachers to grapple with! 😉
You are welcome! Let me know how the talk goes.